Компресия на звук

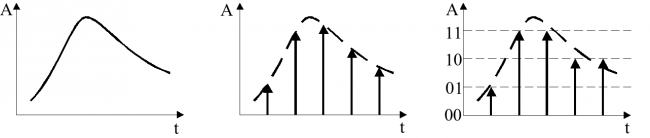
Звукът най-често е в следствие на движение на тяло във някаква среда (въздух,...). Движението предизвиква промяна на налягането, което се разпространява както вълна във водата. Тъпънчето на ухото преобразува промяната на налягането в сигнал, който мозъка ни възприема като звук.

Компютрите използват микрофон вместо тъпанче за преобразуването на звуковото налягане в електрически сигнал. След това на определен интервал от време (примерно - 44000 пъти в sec) се вземат отчети (samples) за стойността на електричския сигнал. Всяко измерване се съхранява като число с фиксирана точност (примерно 8, 16 бита).

Компютрите излъчват звуков сигнал, като съхранети отчети са подават към устройство генериращо електрически сигнал, който се подава към тонколоните.

Самплиране на сигнал

• mp3 player
• GSM телефония

bit rate

Количество битове необходимо за запис на 1 секунда звук.

CD-to има фиксирана семплираща честота =>

44100samples/sec * 16bits/samples = 705600bits/sec

Сравнително големият размер на аудио файловете в CD формат, ни дава основание да търсим по ефективни методи за съхранение на звук.

Компресия със загуби

Оригиналният сигнал се замества от линиейна комбинация на косиносови функции.

...

...

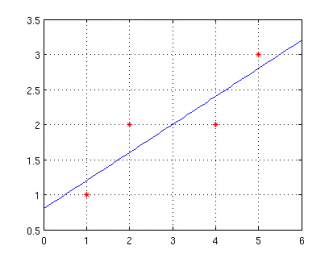
Задача. 1. Да се намери y = f(x) по зададени точки

x = [1 2 4 5];
y = [1 2 2 3];

• Намиране на най-близката функция от първи ред - y = a + b*x

A = [ [1 1 1 1]' , x'];
z = A\y';
%коефиценти на функцията
a = z(1)
b = z(2) 

%генериране на стойности за x
x1 =linspace(0,6,20);
%стойност на функцията за тези стойности
y1 = a + b*x1;
%изчертаване на дадените точки и най-близката права
plot(x1,y1,'-b',x,y,'*r')
grid on

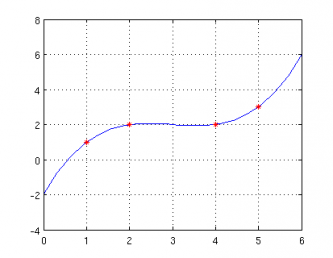
• Намиране на апроксимираща функция от трети ред у = а + b*x + c*x^2 +d*x^3

A = [ [1 1 1 1]' , x', x'.^2, x'.^3];
z = A\y';
%коефиценти на функцията
a = z(1)
b = z(2)
c = z(3)
d = z(4)
x1 =linspace(0,6,20);
%стойност на функцията за тези стойности
y1 = a + b*x1+c*x1.^2+d*x1.^3;
%изчертаване на дадените точки и най-близката права
plot(x1,y1,'-b',x,y,'*r')
grid on

Заместване на (голям) набор от данни с друг (по-малък) набор от моделиращи коефициенти, които заместват данните чрез минимизиране на разликите между модела и данните.

Задача 2. Да разгледаме функцията f(t) = cos(t) + 5 cos(2t) + cos(3t) + 2 cos(4t) в интервала 0 < t < 2pi. В този интервал може да заместим функцията с равномерно взети отчети за стойността на функцията.

%Разделяме периода 2pi на броя отчети които се ползват
t = linspace (0,2*pi,100)';

%За всяка стойност на x намираме f(t)
b = cos(t) + 5*cos(2*t) + cos(3*t) + 2*cos(4*t);
 
%Обратно генериране на коефициентите
%Създаваме линейна система уравнения
A = [ones(size(t)), cos(t), cos(2*t), cos(3*t), cos(4*t)];
y = A\b