Компресия на звук
Звукът най-често е в следствие на движение на тяло във някаква среда (въздух,...). Движението предизвиква промяна на налягането, което се разпространява както вълна във водата. Тъпънчето на ухото преобразува промяната на налягането в сигнал, който мозъка ни възприема като звук.
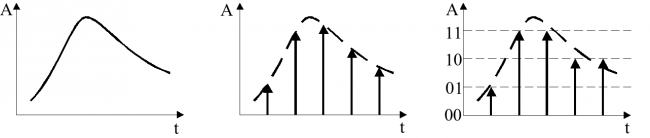
Компютрите използват микрофон вместо тъпанче за преобразуването на звуковото налягане в електрически сигнал. След това на определен интервал от време (примерно - 44000 пъти в sec) се вземат отчети (samples) за стойността на електричския сигнал. Всяко измерване се съхранява като число с фиксирана точност (примерно 8, 16 бита).
Contents
импулсно кодова модулация
- линейно кодиране
- логаритмично кодиране
Дигитализирането по този начин и директното съхраняването на отчетите се нарича линейна импулсно кодова модулация. В такъв формат за записани CD-тата и wav файловете.
Компютрите излъчват звуков сигнал, като съхранети отчети са подават към устройство генериращо електрически сигнал, който се подава към тонколоните.
Цифрова обработка на сигналите
[ll Fs] = wavread('LL.wav');
ll = 0.07413 0.04541 0.06058 0.02930 0.05316 0.00235 0.04892 -0.02866 0.04269 -0.05762 0.03540 -0.08215 0.02930 -0.10242 0.02271 -0.11783 0.01526 -0.12515 0.00735 -0.12766 -0.00253 -0.13477 -0.01025 -0.14554 -0.01047 -0.15143
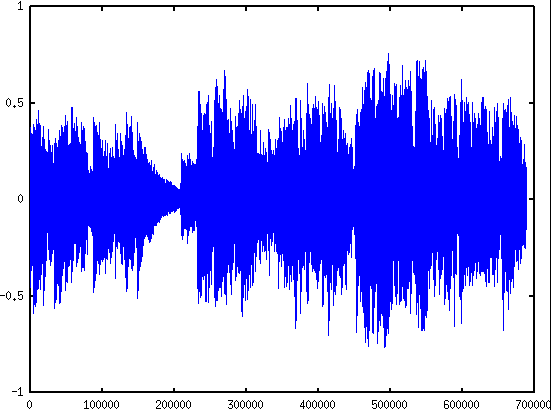
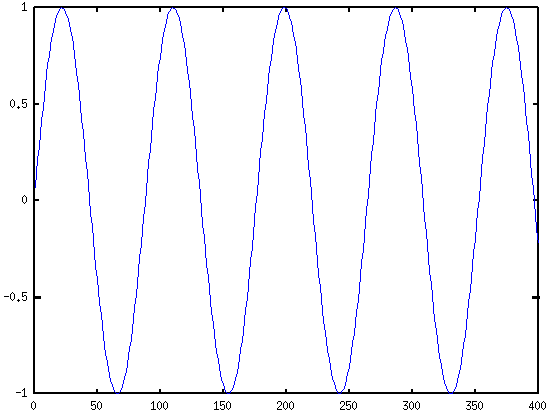
plot(ll(:,1));
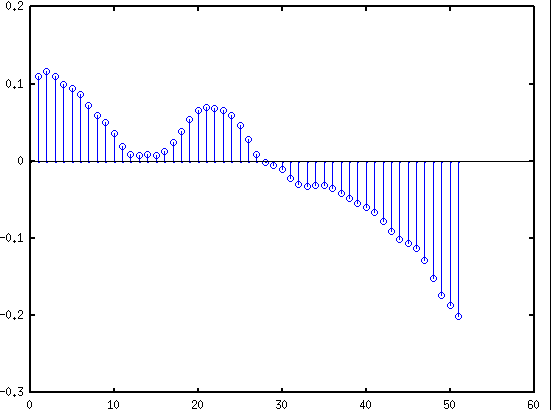
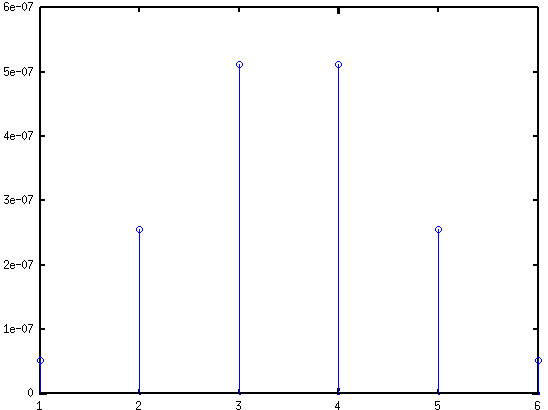
stem(ll(250:300,1));
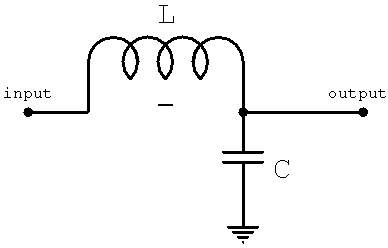
Филтър:
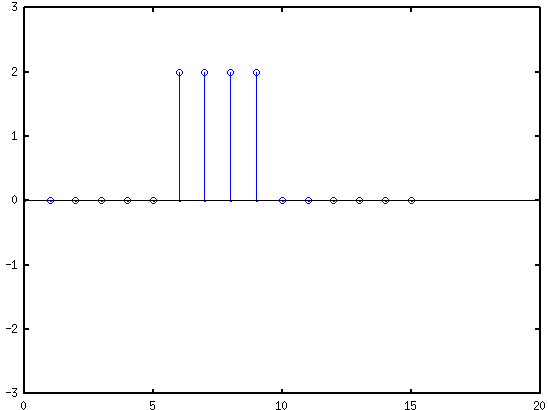
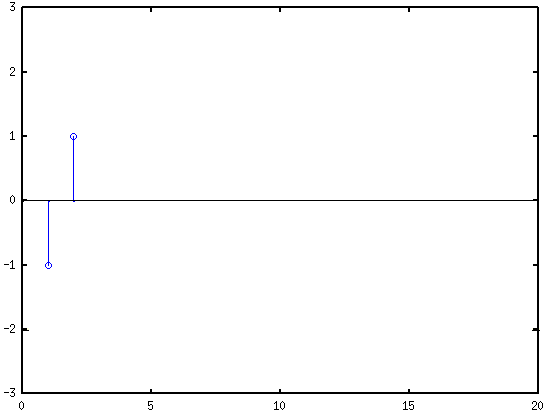
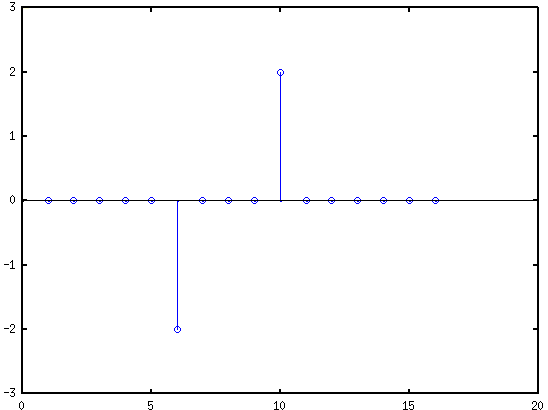
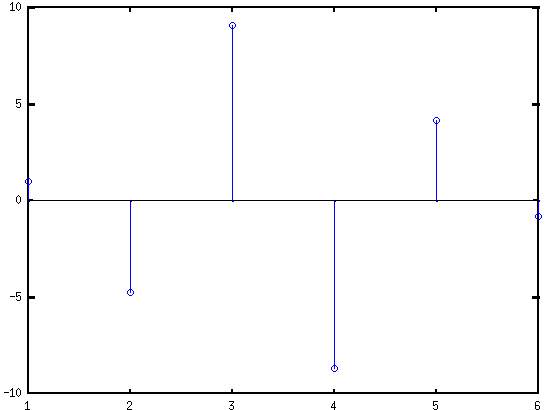
- signal = [0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 ];
- filter = [-1 1]
- conv(signal, filter)
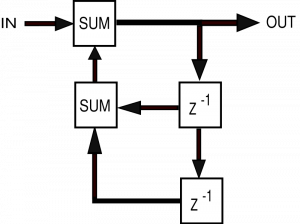
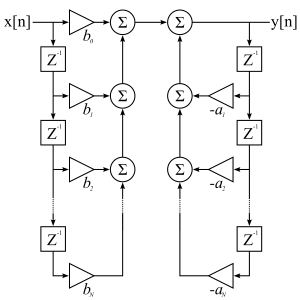
Филтриране IIR
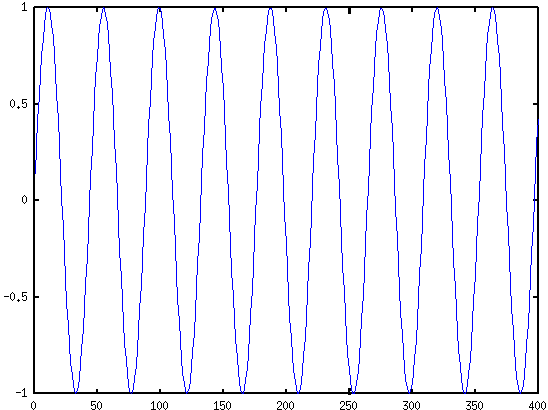
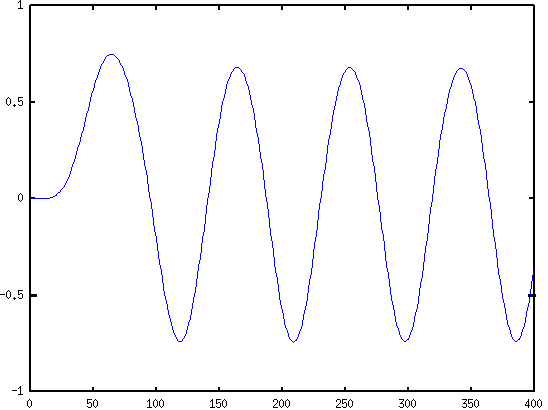
- s1 = sinetone(500,44100,1,1);
- s2 = sinetone(1000,44100,1,1);
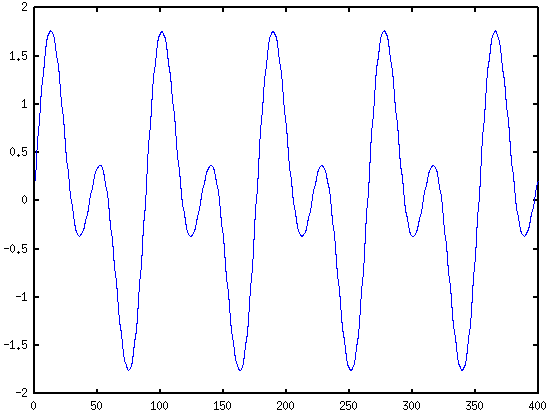
- s = s1+s2
- Филтър
- НЧФ (Ниско Честотен Филтър)
- Fmax = 500;
- Fs = 44100;
- size = 5;
- [b a] = butter(size, 2* Fmax / Fs);
- Входен сигнал
- Филтриран сигнал
- sf = filter(b,a,s);
efekti
- echo = 1/5*Fs;
- LL_echo = zeros( length(ll) + echo);
- LL_echo = [zeros(echo,1)', ll(:,1)'] + [ll(:,1)', zeros(echo,1)'];
- sound(LL_echo, Fs);
Цифрово композиране на музика
A = 110
Fs = 44100
x = zeros(Fs*4, 1);
F = linspace(1/Fs, 1000, 2^12);
fret = 4;
delay = round(Fs/(A*2^(fret/12)));
b = firls(42, [0 1/delay 2/delay 1], [0 0 1 1]);
a = [1 zeros(1, delay) -0.5 -0.5];
zi = rand(max(length(b),length(a))-1,1);
note = filter(b, a, x, zi);
note = note-mean(note);
note = note/max(abs(note));
sound(note,Fs);
[H,W] = freqz(b, a, F, Fs);
hold on
plot(W, 20*log10(abs(H)), 'r');
title('Harmonics of the A string');
legend('Open A string', 'A string on the 4th fret');
bit rate
Количество битове необходимо за запис на 1 секунда звук.
CD-to има фиксирана семплираща честота =>
44100samples/sec * 16bits/samples = 705600bits/sec
Сравнително големият размер на аудио файловете в CD формат, ни дава основание да търсим по ефективни методи за съхранение на звук.
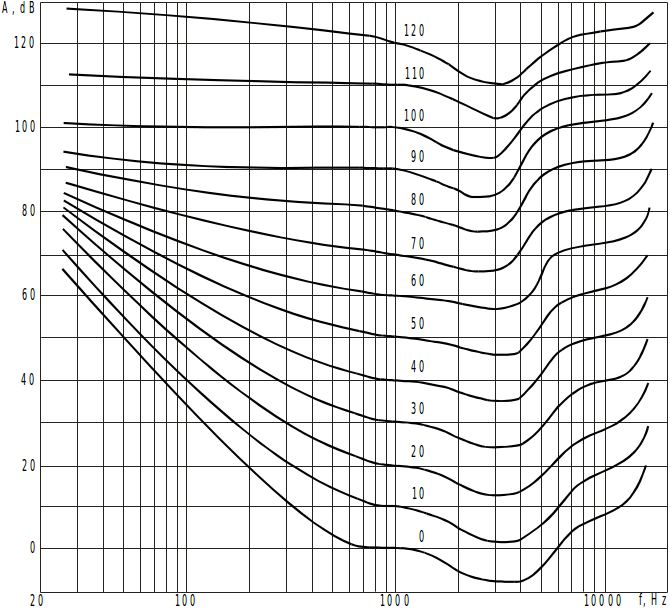
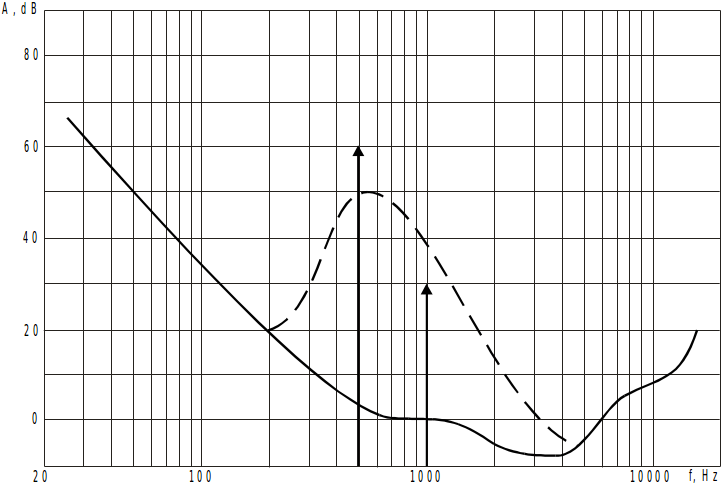
Психоакустичен модел
- Честотен обхват 20 Hz - 20 KHz
- Динамичен диапазон
Компресия без загуби
flac WavePack
Компресия със загуби
- mp3
- GSM телефония
Принцип на работа
Заместване на (голям) набор от данни с друг (по-малък) набор от моделиращи коефициенти, които заместват данните чрез минимизиране на разликите между модела и данните.
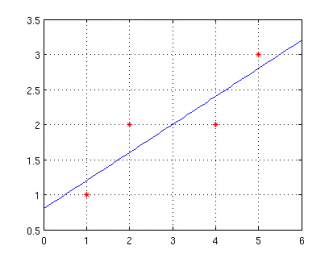
Задача. 1. Да се намери y = f(x) по зададени точки
x = [1 2 4 5]; y = [1 2 2 3];
- Намиране на най-близката функция от първи ред - y = a + b*x
A = [ [1 1 1 1]' , x']; z = A\y'; %коефиценти на функцията a = z(1) b = z(2) %генериране на стойности за x x1 =linspace(0,6,20); %стойност на функцията за тези стойности y1 = a + b*x1; %изчертаване на дадените точки и най-близката права plot(x1,y1,'-b',x,y,'*r') grid on
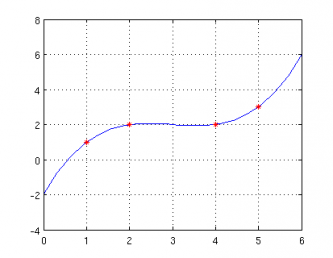
- Намиране на апроксимираща функция от трети ред у = а + b*x + c*x^2 +d*x^3
A = [ [1 1 1 1]' , x', x'.^2, x'.^3]; z = A\y'; %коефиценти на функцията a = z(1) b = z(2) c = z(3) d = z(4) x1 =linspace(0,6,20); %стойност на функцията за тези стойности y1 = a + b*x1+c*x1.^2+d*x1.^3; %изчертаване на дадените точки и най-близката права plot(x1,y1,'-b',x,y,'*r') grid on
Заместващи функции
Оригиналният сигнал се замества от линиейна комбинация на косиносови функции.
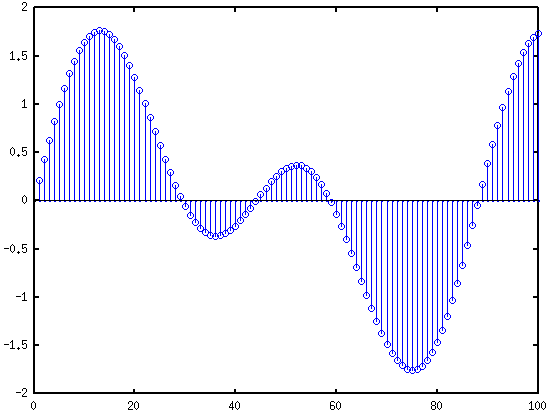
Задача 2. Да разгледаме функцията f(t) = cos(t) + 5 cos(2t) + cos(3t) + 2 cos(4t) в интервала 0 < t < 2pi. В този интервал може да заместим функцията с равномерно взети отчети s за стойността на функцията.
%Разделяме периода 2pi на броя отчети които се ползват t = linspace (0,2*pi,50)'; % t = 0, pi/50, 2pi/50, 3pi/50 ... 50pi/50 %За всяка стойност на s = f(t) s = cos(t) + 5*cos(2*t) + cos(3*t) + 2*cos(4*t); %(1) %Обратно генериране на коефициентите %Създаваме линейна система уравнения A = [cos(0*t), cos(t), cos(2*t), cos(3*t), cos(4*t)]; z = A\s %За решения се получават същите коефициенти като в %(1) plot(t,s);
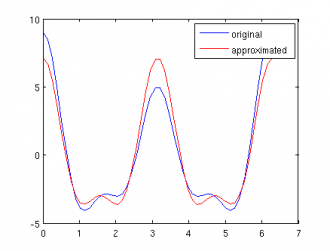
Заместваща функция: Коефициентите пред cos(0*t),cos(t) и cos(3*t) са малки, затова ги игнорираме.
A = [cos(2*t), cos(4*t)]; z = A\s s = z(1)*cos(2*t) + z(2)*cos(4*t); hold; plot(t,s,'r');
Обработка на звук в MATLAB
1. Звуков файл в ЛИКМ формат.
http://ilianko.com/audio/audio.wav
2. Прочитане на звуковия файл.
[s, Fs] = wavread('audio.wav');
% s - стойност на отчет
% Fs - стойност семплиращата честота
3. Възпроизвеждане на звук
sound(s, Fs); plot(s, (0:length(s))/Fs)
Семплираният звук изглежда по-сложен от разглежданите по-горе примери. Въпреки това данните биха могли да се да се апроксимират по подобен начин. За базовa функция ще се използва косиносова функция. Моделиращата функция би изглеждала така:
y = c0 + c1*cos(ω*t) + c2cos(2*ω*t) + · · · + cn−1*cos((n-1)*ω*t)
Като максималната честота (n-1)*ω според теоерамата на Котелников-Шeнон-Найкуист, трябва да е два пъти по-голяма от честотата на семплирания сигнал.
Изчисляване на модел с ДПФ(DCT)
Нека s съдържа една секунда семплиран звук, с честота на семплиране Fs . В този случай s има Fs наброй стойности.
То моделът би трябвало да се намери по този начин:
t = linspace(0,1,Fs); % време на отчета А = [cos(0*2*pi*t)), cos(1*2*pi*t), cos(2*2*pi*t), cos(3*2*pi*t), ..., cos((Fs/2-1)*2*pi*t)]; x = A\b;
...(44100 x 22050)
x = dct(s); Fs = 44100; t = linspace (0,1,Fs)'; s = cos(2*pi*t) + 5*cos(2*2*pi*t) + cos(3*2*pi*t) + 2*cos(4*2*pi*t); x = dct(s); w = sqrt(2/Fs); f = linspace(0, Fs/2, Fs)'; plot (f(1:10),w*x(1:10),'x');
реконструкция на оригиналния сигнал
y = idct(x);
Цифров филтър
[s,Fs] = wavread ('abc.wav');
s = s/max(s);
N = length(s);
x = dct(s); % изчисляване на апроксимиращия модел
w = sqrt(2/N);
f = linspace(0,Fs/2,N)';
plot (f,w*x); % визуализира коефициентите на съществуващите честоти
hold on
m = (f<3000); % генериране на маска за честотите на 3000 Hz
plot (f,w*m.*x,'r');
y = idct(m.*x); % обратна трансформация, без филтрираните честоти
sound(y,Fs);
Задача: Експеримментирайте с няколко стойности на режащата честота
Задача: Създайте маска, която да режи честотите между 200 и 5000 Херца
Идея на mp3
В мп3 вместо отрязване на честотната лента, честотите с по малка значимост се предствавят с по-малка прецизност. Честоти с по малка значимост са тези, чиито коефициенти са с относително малка стойност.
Примерно коефициенти с висока прецизност ще се съхраняват с 16 бита, а тези с малка с 8
Функция за квантуване
function y = quantize (x, bits) m = max(abs(x)); y = x/m; y = floor((2^bits - 1)*y/2); y = 2*y/(2^bits -1); y = m*y;
Примерна компресия
% Зареждане на аудио файл
[s, Fs] = wavread ('audio.wav');
% Извличане на 10 сек.
s = s(44100*20:44100*30,1);
N = length(s);
% Преминаване в честототмна област
x = dct(s);
w = sqrt(2/N);
f = linspace(0,Fs/2,N)';
% Коефициенти
plot (f,w*x)
pause;
% прагова стойност
cutoff = 1
mask = (abs(w*x)<cutoff);
low=mask.*x;
high=(1-mask).*x;
% Визуализация прагови стойности
plot(f,w*high,'r',f,w*low,'b')
% Кванизация
lowbits=8
low = quantize(low, lowbits);
% Реконструиране на сигнала!
y=idct(low+high);
sound (y,Fs);