Difference between revisions of "Компресия на звук"
| Line 23: | Line 23: | ||
== Компресия със загуби == | == Компресия със загуби == | ||
| − | + | Заместване на (голям) набор от данни с друг (по-малък) набор от моделиращи коефициенти, които заместват данните чрез минимизиране на разликите между модела и данните. | |
[[Image:line.png|right|thumb|333px|...]] | [[Image:line.png|right|thumb|333px|...]] | ||
[[Image:cubic.png|right|thumb|333px|...]] | [[Image:cubic.png|right|thumb|333px|...]] | ||
| + | |||
Задача. 1. Да се намери y = f(x) по зададени точки | Задача. 1. Да се намери y = f(x) по зададени точки | ||
x = [1 2 4 5]; | x = [1 2 4 5]; | ||
| Line 47: | Line 48: | ||
plot(x1,y1,'-b',x,y,'*r') | plot(x1,y1,'-b',x,y,'*r') | ||
grid on | grid on | ||
| + | |||
*Намиране на апроксимираща функция от трети ред у = а + b*x + c*x^2 +d*x^3 | *Намиране на апроксимираща функция от трети ред у = а + b*x + c*x^2 +d*x^3 | ||
| Line 63: | Line 65: | ||
grid on | grid on | ||
| − | |||
| + | |||
| + | Оригиналният сигнал се замества от линиейна комбинация на косиносови функции. | ||
Задача 2. | Задача 2. | ||
Да разгледаме функцията '' '''f(t) = cos(t) + 5 cos(2t) + cos(3t) + 2 cos(4t)''' '' в интервала 0 < t < 2pi. | Да разгледаме функцията '' '''f(t) = cos(t) + 5 cos(2t) + cos(3t) + 2 cos(4t)''' '' в интервала 0 < t < 2pi. | ||
| Line 72: | Line 75: | ||
%Разделяме периода 2pi на броя отчети които се ползват | %Разделяме периода 2pi на броя отчети които се ползват | ||
t = linspace (0,2*pi,50)'; | t = linspace (0,2*pi,50)'; | ||
| − | + | ||
%За всяка стойност на x намираме f(t) | %За всяка стойност на x намираме f(t) | ||
b = cos(t) + 5*cos(2*t) + cos(3*t) + 2*cos(4*t); | b = cos(t) + 5*cos(2*t) + cos(3*t) + 2*cos(4*t); | ||
| − | + | ||
%Обратно генериране на коефициентите | %Обратно генериране на коефициентите | ||
%Създаваме линейна система уравнения | %Създаваме линейна система уравнения | ||
A = [ones(size(t)), cos(t), cos(2*t), cos(3*t), cos(4*t)]; | A = [ones(size(t)), cos(t), cos(2*t), cos(3*t), cos(4*t)]; | ||
y = A\b | y = A\b | ||
Revision as of 03:31, 28 September 2012
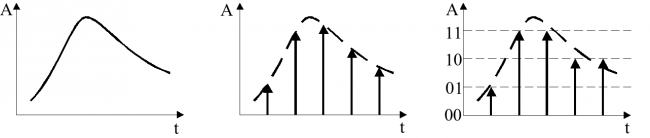
Звукът най-често е в следствие на движение на тяло във някаква среда (въздух,...). Движението предизвиква промяна на налягането, което се разпространява както вълна във водата. Тъпънчето на ухото преобразува промяната на налягането в сигнал, който мозъка ни възприема като звук.
Компютрите използват микрофон вместо тъпанче за преобразуването на звуковото налягане в електрически сигнал. След това на определен интервал от време (примерно - 44000 пъти в sec) се вземат отчети (samples) за стойността на електричския сигнал. Всяко измерване се съхранява като число с фиксирана точност (примерно 8, 16 бита).
Компютрите излъчват звуков сигнал, като съхранети отчети са подават към устройство генериращо електрически сигнал, който се подава към тонколоните.
- mp3 player
- GSM телефония
bit rate
Количество битове необходимо за запис на 1 секунда звук.
CD-to има фиксирана семплираща честота =>
44100samples/sec * 16bits/samples = 705600bits/sec
Сравнително големият размер на аудио файловете в CD формат, ни дава основание да търсим по ефективни методи за съхранение на звук.
Компресия без загуби
Компресия със загуби
Заместване на (голям) набор от данни с друг (по-малък) набор от моделиращи коефициенти, които заместват данните чрез минимизиране на разликите между модела и данните.
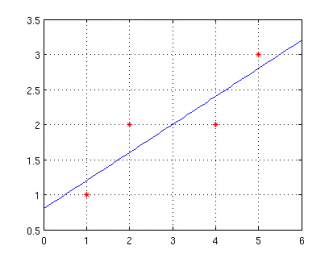
Задача. 1. Да се намери y = f(x) по зададени точки
x = [1 2 4 5]; y = [1 2 2 3];
- Намиране на най-близката функция от първи ред - y = a + b*x
A = [ [1 1 1 1]' , x']; z = A\y'; %коефиценти на функцията a = z(1) b = z(2) %генериране на стойности за x x1 =linspace(0,6,20); %стойност на функцията за тези стойности y1 = a + b*x1; %изчертаване на дадените точки и най-близката права plot(x1,y1,'-b',x,y,'*r') grid on
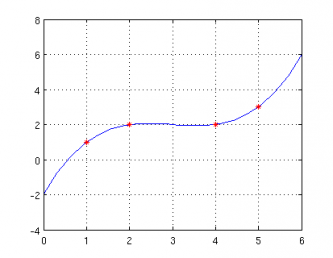
- Намиране на апроксимираща функция от трети ред у = а + b*x + c*x^2 +d*x^3
A = [ [1 1 1 1]' , x', x'.^2, x'.^3]; z = A\y'; %коефиценти на функцията a = z(1) b = z(2) c = z(3) d = z(4) x1 =linspace(0,6,20); %стойност на функцията за тези стойности y1 = a + b*x1+c*x1.^2+d*x1.^3; %изчертаване на дадените точки и най-близката права plot(x1,y1,'-b',x,y,'*r') grid on
Оригиналният сигнал се замества от линиейна комбинация на косиносови функции. Задача 2. Да разгледаме функцията f(t) = cos(t) + 5 cos(2t) + cos(3t) + 2 cos(4t) в интервала 0 < t < 2pi. В този интервал може да заместим функцията с равномерно взети отчети за стойността на функцията.
%Разделяме периода 2pi на броя отчети които се ползват t = linspace (0,2*pi,50)'; %За всяка стойност на x намираме f(t) b = cos(t) + 5*cos(2*t) + cos(3*t) + 2*cos(4*t); %Обратно генериране на коефициентите %Създаваме линейна система уравнения A = [ones(size(t)), cos(t), cos(2*t), cos(3*t), cos(4*t)]; y = A\b