Упражнение 4. Matlab
From Ilianko
Contents
Смесени частни производни
Matlab няма собствена функция. Трябва да се използват собствени програми включващи diff().
Pregled
Definirani simwolni nizowe
x = sym('x')
A = sym('[a, b; c, d]'); - символна матрица
eq = sym('a*x^2 + y');
syms x y a b c;
f = (x+b); - всеки израз имащ символни променливи става символен
Aritmetika с променлива точност
vpa(expr), vpa(expr, 20) - rezultat с 20 значещи цифри digits(50)
Преобразовнания
А = [1/2 ....
S = sym(A) - double-> symbolic
V = vpa(S) - symbolic -> 32 бита точност
А = double(S) - symbolic -> double
Опростяване
collect() simple() subs() simplify()
sub(expr, old, new)
Линейна алгебра
det() inv() poly()
syms b1 b2 b3
b = [ b1; b2; b3] ;
x = A\B - решаване система уравнения
[v, E] = eig(A) собствени стойност - собствени честоти на трептене!
Решаване уравнения
solve(f,x) sym x y; [x y] = solve(f1, f2, x, y) - решава системата f1(x,y) = 0 ; f2(x,y) = 0
Matemati`eski анализ
limit(f, x, a); - granica na f при х клонящо към а
diff(f,x) int(f,x) - неопределен интеграл int(f,x,a,b) - определен интеграл
symsum( f(k), k , n ,m) - suma taylor( f, n, x, a ) - ред на тейлор
Аналитично решаване на ОДУ
y = dsolve('deq', 'x') - общо решение y = dsolve('deq', 'inic', 'x') - частно решение
Система ОДУ
[y1, y2, y3 ...] = dsolve = ('deq1', 'deq2', ..., 'inic1', 'inic2',... , 'x')
Пример:
Махало аналитично решение ОДУ с Matlab ay + by' + cy = 2sin(x), y0(x) = y0 ....
Диференциране
>> syms x y; >> f = exp(-x/y)*sin(x*y) f = sin(x*y)/exp(x/y) >> diff(f,x,2) % втора производна по x ans = sin(x*y)/(y^2*exp(x/y)) - (2*cos(x*y))/exp(x/y) - (y^2*sin(x*y))/exp(x/y)
>> simplify(diff(diff(f,x,2), y, 2)) ans = (x^2*sin(x*y) + 6*y^2*sin(x*y) - 2*y^6*sin(x*y) - 6*x*y*sin(x*y) - 4*x*y^7*cos(x*y) - 2*x*y^5*sin(x*y) + 2*x^2*y^4*sin(x*y) + x^2*y^8*sin(x*y))/(y^6*exp(x/y))
Заместване
>> subs(ans, {x,y}, {1.23, pi/2})
ans =
1.9785
Обединяване на стринг
>> str1 = 'x = ';
>> str2 = 'sin(pi/2)';
>> str = [str1, str2]
str =
x = sin(pi/2)
>> eval(str)
x =
1
Съставяне на функции с променлив брой рагументи
function [a b] = in2out3(x,y,z)
if nargout == 1 %един изходен аргумент
switch nargin % брой входящи аргументи
case 1
a = x;
case 2
a = x+y;
case 3;
a = x +y + z;
end
else
switch nargin
case 1
a = x;
b = x*x;
case 2;
a = x+y;
b = x*x+y*y;
case 3;
a = x+y+z;
b = x*x+y*y+z*z;
end
end
end
Неограничен брой на входни и изходни параметри
function d = var(f, varargin)
% neograniчen брой променливи
n = length(varargin);
for i = 1:n
var = varargin{i} % ! индексът е с големи скоби
syms var;
end
for i = 1:n
f= diff(f,varargin{i});
end
d = f;
end
>> syms x y >> var(f,x,y) var = x var = y ans = cos(x*y)/exp(x/y) + sin(x*y)/(y^2*exp(x/y)) - ... (x*y*sin(x*y))/exp(x/y) - (x*sin(x*y))/(y^3*exp(x/y))
Решаване на интеграли
>> syms x >> int(x) ans = x^2/2
Определен интеграл
>> syms a b x >> int(x, a, b) ans = b^2/2 - a^2/2
syms a b c d x y; >> Ix = int(y*sin(x),x, a, b) Ix = y*(cos(a) - cos(b)) >> Ixy = int(Ix, y, c, d) Ixy = -((c^2 - d^2)*(cos(a) - cos(b)))/2
Символно сумиране
>> syms k; S = symsum(1/k^2, k, 1, inf) S = pi^2/6
Ред на тейлор
>> syms x y >> f = 1/(x^2 + y); >> tf = taylor(f , 7, x) tf = x^4/y^3 - x^2/y^2 - x^6/y^4 + 1/y
>> pretty(taylor(f , 7, y)) 2 3 4 5 6 y y y y y y 1 -- - -- + --- - --- + --- - -- + -- 6 8 10 12 14 4 2 x x x x x x x
Диференциране на членове на матрици
clear
>> syms x k
>> A = [sin(k*x), cos(k*x);sinh(k*x), cosh(k*x)]
A =
[ sin(k*x), cos(k*x)]
[ sinh(k*x), cosh(k*x)]
>> diff(A)
ans =
[ k*cos(k*x), -k*sin(k*x)]
[ k*cosh(k*x), k*sinh(k*x)]
решаване със subs
първи начин
>> subs(A, {k, x} ,{ 2, pi/3})
ans =
0.8660 -0.5000
3.9987 4.121
втори начин
>> k = 2; x = pi/3; >> subs(A) ans = 0.8660 -0.5000 3.9987 4.1218
Решаване на обикновени диференциални уравнения с dsolve()
>> y = dsolve('Dy+y^2 = x^(-2)', 'y(0.5) = -1', 'x') % уравнение, начално условие, решено по х
y =
(5^(1/2)/2 + 1/2)/x - 1/((5^(1/2)*x)/5 + (2*x*x^(5^(1/2))*(1/(5^(1/2) + 2) - 5^(1/2)/10))/(1/2)^(5^(1/2)))
mapl
>> sol = dsolve('Dx=3*x+4*y, Dy = -4*x+3*y', 'x(0) = 0, y(0) = 1', 't')
sol =
x: [1x1 sym]
y: [1x1 sym]
>> sol.x
ans =
sin(4*t)*exp(3*t)
>> sol.y
ans =
cos(4*t)*exp(3*t)
>> subs(sol.x, 't', 0)
ans =
0
>> subs(sol.y, 't', 0)
ans =
1
>> y = dsolve('D3y=y', 'y(0) =1, Dy(0)=-1, D2y(0)=pi','x')
y =
(pi*exp(x))/3 - (cos((3^(1/2)*x)/2)*(pi/3 - 1))/exp(x/2) - (3^(1/2)*sin((3^(1/2)*x)/2)*(pi + 1))/(3*exp(x/2))
>>
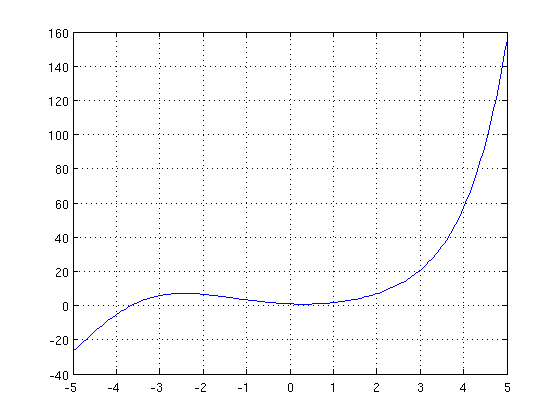
>> X = -5:0.05:5;
>> Y = subs(y,'x',X);
>> plot(X,Y), grid on