Difference between revisions of "Числено интегриране"
| Line 128: | Line 128: | ||
\begin | \begin | ||
I \approx \int_{x_0}^{x_1} L_1 (x)\,dx = \int_{x_0}^{x_1} \left ( y_0 \frac{x-x_1}{-h} +y_1 \frac{x-x_0}{h} \right ) \,dx = \\ | I \approx \int_{x_0}^{x_1} L_1 (x)\,dx = \int_{x_0}^{x_1} \left ( y_0 \frac{x-x_1}{-h} +y_1 \frac{x-x_0}{h} \right ) \,dx = \\ | ||
| − | + | \approx \int_{x_0}^{x_1} y_0 \frac{x-x_1}{-h} \,dx + \int_{x_0}^{x_1} y_1 \frac{x-x_0}{h} \,dx = \\ | |
| − | + | = a^2+2ab+b^2 \\ | |
\end | \end | ||
Revision as of 12:21, 6 January 2013
Contents
В числения анализ, числено интегриране определя група от алгоритми за намиране стойността на определен интеграл. Понятието се използва и при численото решаване на диференциални уравнения.
Идеята на численото интегриране е функцията f(x) да се приближи с подходяща функция φ(x), която по-лесно може да се интегрира. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \phi(x) + r(x)} , където:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(x)} може да се интегрира точно
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(x)} e остатъка (грешката - residual)
Най-често φ(x) е интерполационен полином построен по някакви възли в интервала Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} за Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} .
Числените методи за интегриране се налага да се използват:
- Когато не съществува примитивна функция за f(x) (интегралът не се изразява с елементарни функции)
- когато примитивната функция за f(x) е много сложен израз
Ако f(x) е плавно изменяща се функция, която може да се интегрира в малък брой измерения и има определени гранични стойности, съществуват редица методи с различна степен на точност за апроксимиране на интеграла Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)\,dx} .
Представяме интеграла по следния начин:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)\,dx = \sum_{i=1}^{n} A_i f(x_i) + R(f) }
.
Формули на Нютон-Коутс за числено интегриране
Пример. Да се пресметне по формулата на десните правоъгълници
Решение. По условие Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b] = [2,3]; n=10}
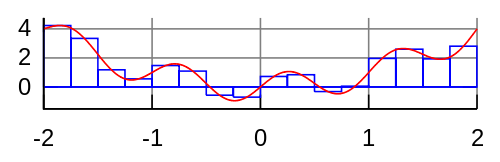
Метод на правоъгълниците
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = \frac{b - a}{n} = \frac{3-2}{10} = 0.1}
Съгласно Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I \approx \int_{a}^{b} = \int_{x_0}^{x_1} + \int_{x_1}^{x_2} + ... + \int_{x_{n-1}}^{x_n} = y_0 h + y_1 h +...+ y_{n-1} h = h \sum_{i=0}^{n-1} y_i}
x = {2, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3}
y = {0.346574, 0.353303, 0.35839, 0.362134, 0.364779, 0.366516,0.367504, 0.367871, 0.367721, 0.367142, 0.366204}.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I \approx h \sum_{i=0}^{n-1} y_i = 0.362193}
Аналитично решение
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_2^3 \frac{log(x)}{x} dx = 1/2 (log^2(3)-log^2(2)) \approx 0.363248}
Решение с Матлаб
h = 0.1 % step
m = 0; % sum
for i = 2:h:3-h
m = log(i)/i + m
end
I = m*h
I = 0.36219
Оценка на грешката
Грешка от интегриране: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert r_0 \vert \leq \left | \int_{x_0}^{x_1} R_0\,dx\ \right | \leq M_1 \left | \int_{x_0}^{x_1} (x-x_0)\,dx\ \right | = M_1 \frac{ (x-x_0)^2 }{2} \Bigg|_{x_0}^{x_1} = M_1 \frac{h^2}{2} = O(h^2) }
Сумарна грешка:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R \leq n*M_1 \frac{h^2}{2} = M_1 \frac{h(b-a)}{2} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1=\max\limits_{[2,3]}\vert f'(\xi)\vert}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=\frac{ln(x)}{x}} за Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{1-ln(x)}{x^2}}
Максималната стойност в [2,3] на Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{1-ln(x)}{x^2}} е при x = 2
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1 = \frac{1 - ln(2)}{2^2} = 0.077 }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = M_1 \frac{h(b-a)}{2} = 0.077*0.1/2 = 0.004}
Анализ
Разликата от аналитичното решение и численото решение е Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.3632 - 0.3621 = 0.0011} , което е в рамките на максималната грешка.
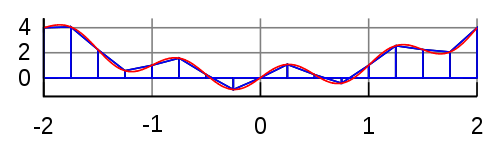
Формула на трапеца
Геометрично извеждане
Идеята на геометричното извеждане е да замести площта под кривата y = f(x) за x = a до х = b с площта на трапец ограничена от точките (a, 0), (b, 0), [a, f (a)], и [b, f (b)].
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x) \,dx \approx \frac{b-a}{2} \left [ f(a) + f(b) \right ]}
Правилото на трапеца няма как да е точно за големи интервали, но ако разглежданият интервал се раздели на по-малки интервали и се сумират техните стойности ще се получи сравнително точно заместване. Ако функцията f има втора производна то грешката от интегриране намалява с Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h^2 } , където h e големината на интеграла.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)dx \approx h \left ( \frac{f(x_0)}{2} +f(x_1) + \dots + f(x_{n-1}) + \frac{f(x_n)}{2} \right ) }
Аналитично извеждане
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_1(x) = y_0 \frac{x-x_1}{x_0-x_1}+y_0 \frac{x-x_1}{x_1-x_0} <=> L_1(x) = y_0 \frac{x-x_1}{h}+y_0 \frac{x-x_1}{h} }
грешка на приближението Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1(x) = \frac{f''(\xi)}{2}(x-x_0)(x-x_1) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | R_1(x) | \leq \frac{M_2}{2} \left | (x-x_0)(x-x_1) \right | } , където
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_2 = \max\limits_{[a,b]} \left | f''(\xi) \right | }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = L_1(x) + R_1(x) }
Интегрираме в интервала Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x_0,x_1],\, I = \int_{x_0}^{x_1} f(x)\,dx = \int_{x_0}^{x_1} L_1 (x)\,dx + \int_{x_0}^{x_1} R_1 (x) \,dx }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin(align) \\ & \approx \frac{y_0}{-h}\int_{x_0}^{x_1} (x-x_1) \,dx + \frac{y_1}{h}\int_{x_0}^{x_1} (x-x_0) \,dx = \\ \end(align) & = \frac{y_0}{-h} \frac{(x-x_1)}{2} \Bigg |_{x_0}^{x_1} + \frac{y_1}{h} \frac{(x-x_0)^2}{2} \Bigg |_{x_0}^{x_1} = h \frac{(y_0+y_1)}{2} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin I \approx \int_{x_0}^{x_1} L_1 (x)\,dx = \int_{x_0}^{x_1} \left ( y_0 \frac{x-x_1}{-h} +y_1 \frac{x-x_0}{h} \right ) \,dx = \\ \approx \int_{x_0}^{x_1} y_0 \frac{x-x_1}{-h} \,dx + \int_{x_0}^{x_1} y_1 \frac{x-x_0}{h} \,dx = \\ = a^2+2ab+b^2 \\ \end }