Difference between revisions of "Изкуствени невронни мрежи"
| Line 74: | Line 74: | ||
==Видове мрежи== | ==Видове мрежи== | ||
===Мрежи на Хопфийлд=== | ===Мрежи на Хопфийлд=== | ||
| + | В модела на Хопфийлд всеки неврон е свързан с всеки друг неврон. Потокът от информация в тази мрежа не е в едно направление. Възможно е информацията от възел да се върне през други възли към същия възел. Това означава, че мрежата е с обратна връзка и се нарича още рекурсивна мрежа. | ||
| + | |||
| + | |||
| + | |||
| + | Матрицата на връзките се описва с: | ||
| + | <math>{W_{ik}}= \frac{1}{N} Summ Xim Xkm</math> | ||
| + | където N е брой неврони, Xkm е стойността на неврон k в набор m и sum е за всички набори от m=1 to m=p. Обучението е с правилото на Неб. Обучаващото правило работи добре, когато наборите, които трябва да се записват са произволни с еднаква вероятност за the patterns that are to be stored are random patterns with equal probability (+1) и (-1). В големи мрежи (N клони към безкрайност) броят сучайни набори, които могат да се запазват е приблизително 0.14 по N. | ||
| + | |||
===Обикновени перцептрони=== | ===Обикновени перцептрони=== | ||
===Многослойни мрежи=== | ===Многослойни мрежи=== | ||
===Мешини на Болцман=== | ===Мешини на Болцман=== | ||
===Самообучаващи се мрежи=== | ===Самообучаващи се мрежи=== | ||
Revision as of 18:42, 9 December 2012
Contents
Какво е невронна мрежа
Изкуствена невронна мрежа е математически модел, съставен от набор отделни елементи, които имитират:
- свойства на биологични невронни системи;
- процесите на адаптивно биологично усвояване на нови знания и умения.
При решаване на задачи като:
- разпознаване на говор,
- разпознаване на образи,
- разпознаване по образец и т.н.,
се счита, че невронните мрежи могат да се прилагат успешно.
Съвременният модел на невронна мрежа е композиция на добре взаимодействащи си елементи (аналог на невроните) и свързващите ги канали (аналог на синапсите).
Основно свойство на невронните мрежи е самообучението (само-модификацията).
Човешкият мозък притежава изчислителни свойства, които се доста уникални. Тези свойства сериозно се различават от свойствата на дигиталния компютър. Началото на ИНМ се поставя с изследване на изчислителните следствия на тези различия.
Това води до разработването на нов подход при обработка на данни в изкуствения интелект, вдъхновен от начина, по който това се извършва в човешкия мозък.
Невронните мрежи изучават и прилагат:
- подробни и правдиви модели за реални мозъчни структури;
- висшите и абстрактни свойства на невронни изчисления.
Неврони
http://bg.wikipedia.org/wiki/Неврон
Основни елементи на невронните мрежи
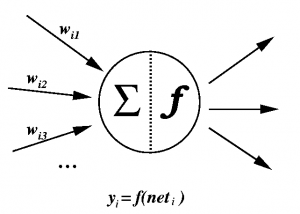
Основният обработващ елемент в изкуствените невронни мрежи е изкуственият неврон. Той не съответства напълно на биологичните неврони. На фигурата по-долу е представен изкуствен неврон.
Всеки неврон получава входен сигнал от съседни неврони или други източници и го използва, за да изчисли изходен сигнал, който предава на други възли в мрежата. Различават се три типа възли в невронната мрежа:
- входни възли, които получават данни от средата, в която работи системата;
- изходни възли, които изпращат данни навън от системата;
- скрити възли, чиито входни и изходни сигнали са в мрежата.
Обработката на информацията, която се извършва от неврона може да се представи със следния израз:
,
където i се променя от 0 до n. С w е означен тегловният коефициент на връзката между тялото и дендритите на неврона; с yj е означена активността на невроните, свързани с неврон i, yi е изходът на неврона, f е предавателна функция, wij е тегловният коефициент между неврон i и неврон j.
Ако стойността на теглото wij е положителна, връзката е възбуждаща, в противен случай е подтискаща.
Обикновено предавателната функция е ненамаляваща функция на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция.
Мрежови архитектури
В зависимост от вида на връзките между невроните мрежите са:
- прави мрежи - данните се предават от входните към изходните възли без обратни връзки. Мрежата може да бъде от един или няколко слоя;
- рекурсивни мрежи - има и обратни връзки. Динамичните свойства на тези мрежи са важни. При обучение невроните са с неопределена активност, която се променя докато мрежата достигне състояние, в което не настъпват повече значителни промени. В рекурсивните мрежи няма разлика между вход и изход, по-скоро има набор от видими неврони, които комуникират със средата и набор от скрити неврони, които нямат подобна функция.
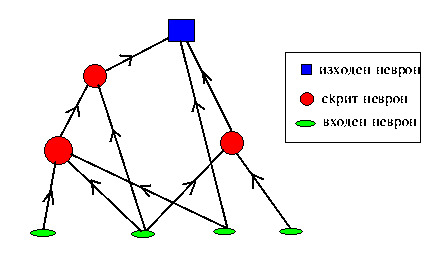
Класически пример за права мрежа е перцептронът.
Типична рекурсивна мрежа е дадена на фигурата по-долу.
Обучение на невронни мрежи
Според вида на управление обучението бива:
- обучение с учител или асоциативно обучение, при което на мрежата се предоставят входният и съответният му изходен образец. Обучаващите входно-изходни двойки се предоставят от учител или от системата, включваща мрежата. Теглата се уточняват като се се използва разликата между стойностите на изходните неврони при зададен входен образец и стойностите на тези възли, които трябва да се получат при коректна работа на мрежата.
- обучение без учител или самоорганизация, при което изходните неврони се обучават да отговарят на набори от входни образци. Передварително няма множество от категории, към които да се класифицират входните образци. Системата сама открива най-характерните черти на входните набори и изработва свое собствено представяне на входните стимули.
Обучението на невронните мрежи се извършва по алгоритъм, включващ правило, което модифицира теглата на връзките между невроните. Съществуват две правила, които могат да се модифицират за обучение на различни мрежи:
- правило на Хеб - теглото на връзката между неврони i и j, където неврон i получава вход от неврон j, се увеличава пропорционално на произведението от активностите на неврони i и j.
- правило на Уидроу-Хоф или делта правило - теглото на връзката между неврони i и j, където неврон i получава вход от неврон j, се увеличава пропорционално на произведението от разликата на желаната и действителната активност на неврон i и активността на неврон j.
Видове мрежи
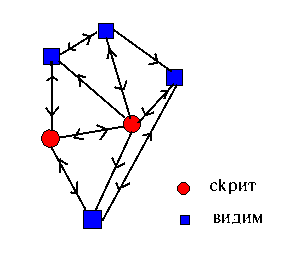
Мрежи на Хопфийлд
В модела на Хопфийлд всеки неврон е свързан с всеки друг неврон. Потокът от информация в тази мрежа не е в едно направление. Възможно е информацията от възел да се върне през други възли към същия възел. Това означава, че мрежата е с обратна връзка и се нарича още рекурсивна мрежа.
Матрицата на връзките се описва с:
където N е брой неврони, Xkm е стойността на неврон k в набор m и sum е за всички набори от m=1 to m=p. Обучението е с правилото на Неб. Обучаващото правило работи добре, когато наборите, които трябва да се записват са произволни с еднаква вероятност за the patterns that are to be stored are random patterns with equal probability (+1) и (-1). В големи мрежи (N клони към безкрайност) броят сучайни набори, които могат да се запазват е приблизително 0.14 по N.