Difference between revisions of "Изкуствени невронни мрежи"
| Line 46: | Line 46: | ||
Обикновено предавателната функция е [[ненамаляваща функция]] на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция. | Обикновено предавателната функция е [[ненамаляваща функция]] на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция. | ||
| + | |||
| + | |||
| + | ==Мрежови архитектури== | ||
| + | |||
| + | В зависимост от вида на връзките между невроните мрежите са: | ||
| + | *'''прави мрежи''' - данните се предават от входните към изходните възли без обратни връзки. Мрежата може да бъде от един или няколко слоя; | ||
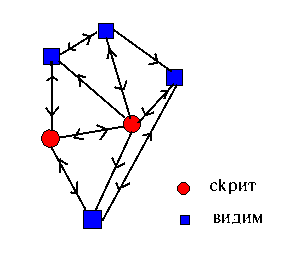
| + | *'''рекурсивни мрежи''' - има и обратни връзки. Динамичните свойства на тези мрежи са важни. При обучение невроните са с неопределена активност, която се променя докато мрежата достигне състояние, в което не настъпват повече значителни промени. В рекурсивните мрежи няма разлика между вход и изход, по-скоро има набор от видими неврони, които комуникират със средата и набор от скрити неврони, които нямат подобна функция. | ||
| + | |||
| + | |||
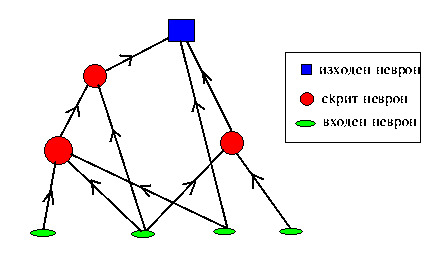
| + | Класически пример за права мрежа е перцептронът. | ||
| + | [[Image:rightNetwork.gif]] | ||
| + | Типична рекурсивна мрежа е дадена на фигурата по-долу. | ||
| + | [[Image:recurentNetwork.gif]] | ||
Revision as of 18:13, 9 December 2012
Структурата на изкуствената невронна мрежа е математически модел, съставен от набор отделни елементи, които имитират:
- свойства на биологични невронни системи;
- процесите на адаптивно биологично усвояване на нови знания и умeния.
При решаване на задачи като:
- разпознаване на говор,
- разпознаване на образи,
- разпознаване по образец и т.н.,
се счита, че невронните мрежи могат да се прилагат успешно.
Съвременният модел на невронна мрежа е композиция на добре взаимодействащи си елементи (аналог на невроните) и свързващите ги канали (аналог на синапсите).
Основно свойство на невронните мрежи е самообучението (само-модификацията).
Човешкият мозък притежава изчислителни свойства, които се доста уникални. Тези свойства сериозно се различават от свойствата на дигиталния компютър. Началото на ИНМ се поставя с изследване на изчислителните следствия на тези различия.
Това води до разработването на нов подход при обработка на данни в изкуствения интелект, вдъхновен от начина, по който това се извършва в човешкия мозък.
Невронните мрежи изучават и прилагат:
- подробни и правдиви модели за реални мозъчни структури;
- висшите и абстрактни свойства на невронни изчисления.
Неврони
http://bg.wikipedia.org/wiki/Неврон
Основни елементи на невронните мрежи
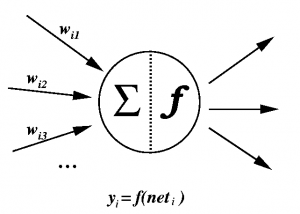
Основният обработващ елемент в изкуствените невронни мрежи е изкуственият неврон. Той не съответства напълно на биологичните неврони. На фигурата по-долу е представен изкуствен неврон.
Всеки неврон получава входен сигнал от съседни неврони или други източници и го използва, за да изчисли изходен сигнал, който предава на други възли в мрежата. Различават се три типа възли в невронната мрежа:
- входни възли, които получават данни от средата, в която работи системата;
- изходни възли, които изпращат данни навън от системата;
- скрити възли, чиито входни и изходни сигнали са в мрежата.
Обработката на информацията, която се извършва от неврона може да се представи със следния израз:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {y_i}=f \left( \sum_{j}{w_{ij}}{y_j} \right) }
,
където i се променя от 0 до n. С w е означен тегловният коефициент на връзката между тялото и дендритите на неврона; с yj е означена активността на невроните, свързани с неврон i, yi е изходът на неврона, f е предавателна функция, wij е тегловният коефициент между неврон i и неврон j.
Ако стойността на теглото wij е положителна, връзката е възбуждаща, в противен случай е подтискаща.
Обикновено предавателната функция е ненамаляваща функция на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция.
Мрежови архитектури
В зависимост от вида на връзките между невроните мрежите са:
- прави мрежи - данните се предават от входните към изходните възли без обратни връзки. Мрежата може да бъде от един или няколко слоя;
- рекурсивни мрежи - има и обратни връзки. Динамичните свойства на тези мрежи са важни. При обучение невроните са с неопределена активност, която се променя докато мрежата достигне състояние, в което не настъпват повече значителни промени. В рекурсивните мрежи няма разлика между вход и изход, по-скоро има набор от видими неврони, които комуникират със средата и набор от скрити неврони, които нямат подобна функция.
Класически пример за права мрежа е перцептронът.
 Типична рекурсивна мрежа е дадена на фигурата по-долу.
Типична рекурсивна мрежа е дадена на фигурата по-долу.