Difference between revisions of "Цифрови камери"
m (moved Упражнение 12. Цифрови камери to Цифрови камери) |
(→Matlab) |
||
| Line 70: | Line 70: | ||
== Matlab == | == Matlab == | ||
| + | |||
| + | Основни функции за работа с изображения: | ||
| + | *'''''imread('file_name')''''' - зареждане на изображение от файл. Ако е цветно избражението ще се зареди в масив (матрица) с размери '''''n*m*3''''', където '''''n''''' и '''''m''''' са размерите на изображението; | ||
| + | *'''''imshow(img)''''' - визуализиране на изображение; | ||
| + | *'''''imwrite(img,'file_name')''''' - запис на избражение във файл; | ||
| + | |||
| + | |||
червен канал | червен канал | ||
<code><pre> | <code><pre> | ||
lena = imread('/home/ilianko/ram/lena_std.tif'); | lena = imread('/home/ilianko/ram/lena_std.tif'); | ||
| − | lena(:,:,3) = 0; | + | lena(:,:,3) = 0; %Нулиране на всички елементи от третото изерение |
| − | lena(:,:,2) = 0; | + | lena(:,:,2) = 0; %Нулиране на всички елементи от второ измерение |
| − | RAW = lena(:,:,1); | + | RAW = lena(:,:,1); %Визулизиране на първо измерение |
imwrite(lena, 'R.tif'); | imwrite(lena, 'R.tif'); | ||
imwrite(RAW, 'BW.tif'); | imwrite(RAW, 'BW.tif'); | ||
Revision as of 09:33, 1 April 2013
Contents
Цел на упражнението
Запознаване с принципа на работа на съвременните цифрови фотоапарати и особеностите при изграждане цветно изображение.
Оптичен сензор на цифров фотоапарат
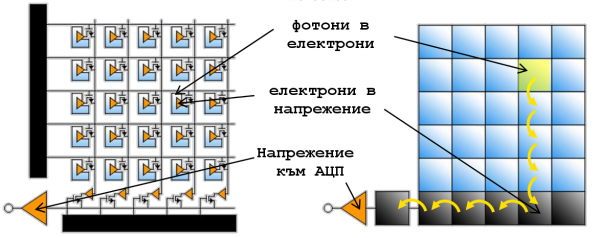
За преобразуване на образа в цифров вид камерите използват оптични сензори, съдържащи милиони елементи подредени в матрица. Всеки елемент сам по себе си е полупроводников оптичен сензор, в който след попадане на светлина, се създава пропорционално на светлината количество свободни електрони. Електроните в последствие се „преброяват“ и преобразуват в цифров сигнал. Съвременните цифровите фотоапарати (камери) разчитат на две технологии за изработка на оптични сензори, които основно се различават по метода, който се използва при преброяването на генерираните електрони. Двете технологии възникват почти едновременно в периода 1960 - 1970 година, но първоначално CCD се оказва по удачно решение и се използва при почти всички фото и видео устройства. С усъвършенстване на литографските технологии при изработка на интегрални схеми и нуждата от ниско енергоемка електроника, след 90-те години на миналия век CMOS технологията за оптични сензори се възражда и в момента до голяма степен CMOS сензорите имат качествата на CCD сензорите, дори по някои параметри ги превъзхождат. CCD – charge coupled device – структура с пренасяне на заряда. Първоначално се разработва за преместващи регистри. CMOS – complementary metal oxyde semiconducture – комплементарна двойка от полеви транзистори, се използва още при изработка на RAM памети и микропроцесори. Основната разлика в принципа на функциониране на сензорите CMOS и CCD е, че при първите произволен пиксел може да бъде достъпен във всеки момент, докато при CCD сензорите достъпът е в последователен ред, подобно на преместващи регистри (фиг 1). CCD матриците имат по-добри шумови характеристики, но изискват по-голяма консумация на енергия.
Цветно изображение
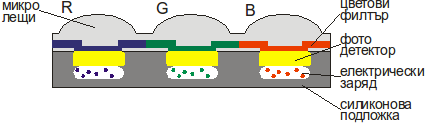
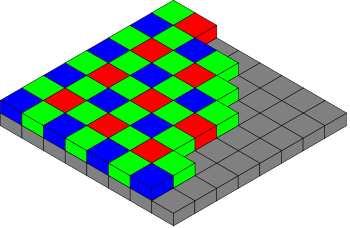
Оптичният сензор регистрира количеството светлина, попаднало върху повърхността му, но информацията за цвета се губи. Освен светлина от видимия спектър оптичния сензор регистрира и фотони от невидимия спектър. От горните два факта следва, че без допълнителна обработка бихме могли да получим само черно бяло изображение. За получаване на цветно изображение се заимства принципа на човешкото възприятие на цвета. Очните нерви са чувствителни единствено към спектъра на червения, зеления и синия цвят. От интензитета на тези цветове се изгражда цялостното цветно възприятие. По подобен начин се получава и цветното изображение в цифровата фотографията - с помощта на цветни филтри или чрез пространствено разделяне на светлината се регистрират единствено стойностите за основните цветове. В първия вариант цветовите филтри се поставят пред всеки един пиксел (фиг. 2), а при втория има три сензорни матрици и оптична система насочваща различните цветове към всеки един от сензорите. В съвременните камери основно се използва един сензор, като подредбата на цветовите филтри се разпределя по определен начин. Най-широко използваната подредба е патентована от Bryce Bayer през 1976 и се нарича Bayer filter (фиг. 3).
Пикселите са групирани по четири, на всеки червен и син има два зелени. Информацията за зеления цвят е най-ценна, защото човешкото окото е най- чувствително към този цвят.
Получената по този начин снимка се нарича Bayer pattern, тя съдържа само 1/3 от информацията на оригиналния образ, затова трябва допълнително да се обработи за възстановяване на пропуснатите пиксели. Това става посредством различни по сложност математически интерполира- щи алгоритми, а процесът се нарича „demosaing“. Фотоапаратите от по-висок клас позволяват запазване на необработената снимка (raw format image) и в последствие тя би могла да се обработи с по-прецизни алгоритми на по-мощен компютър, с цел максимално добро възстановяване на изгубената информация.
Интерполиращи алгоритми
Най-лесният алгоритъм за възстановяване на изгубените пиксели е „копиране на най-близкия съсед“ (nearest neighbor interpolation). Този алгоритъм няма да изисква никакви допълнителни математически операции, а за стойност на неизвестния пиксел се взема същата стойност като на най-близко известния. Следващ вариант по математическа сложност е билинейната интерполация. В този случай се предполага, че изменението на цвета е линейно и се взема средна стойност между два или четирите най-близки известни пиксела. По долу са дадени формулите за възстановяване на цветовете.
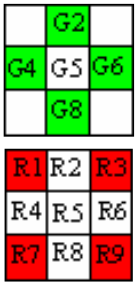
Възстановяване на зеления цвят: Ако са известни стойностите на пиксели G2, G4, G6 и G8 на зеления цвят, то:
G5 = 1/4 * (G2 +G4+G6+G8).
Възстановяване на синия и червения цвят: Ако са известни стойностите на пиксели R1, R3, R7 и R9 на червения или синия цвят, то:
R2 = 1/2*(R1+R3), R4 = 1/2*(R1+R7), R6 = 1/2*(R9+R3), R8 = 1/2*(R9+R7). R5 =1/4*( R1+R3+R9+R7).
Друга възможност, сравнително лесна за реализация, е бикубичната интерполация. При нея стойността на неизвестния пиксел се изчислява от 16 околни пиксела. Проблемът при споменатите интерполации е, че работят добре, само когато снимката няма детайли с резки изменения на цветовете, както например при смяна от черен на бял цвят по ръба на буква. Грешките и разликите, които се получават от интерполацията се наричат артефакти. С цел намаляване на артефактите са създадени група алгоритми с общо название адаптивни. Те изследват структурата на снимката за даден район и в зависимост от резултата вземат под различно внимание стойностите на околните пиксели при изчисляване на неизвестния пиксел в този район.
Задачи за изпълнение
- Визуализирайте поотделно цветните канали на снимка.
- Създайте изкуствена снимка, която да представлява необработено изображение получено от филтър на Байер.
- Възстановете цветовете на снимката, като използвате nearest neighbor интерполация.
- Възстановете снимката, като използвате билинейна интерполация.
- Сравнете субективно и математически оригиналната снимка с получените снимки от задачи 3 и 4.
Начин на работа
За задачите използвайте снимка предоставена в цифров вид от ръководителя на упражнението или свалена от цифров фотоапарат. Всеки студент да работи с различна снимка. За обработката и визуализацията на изображенията може да ползвате библиотеките на openCV за изпълнение на C или Java, или специализираните продукти Matlab и безплатната му алтернатива Octave.
В задача 5 направете субективна оценка, като опишете видимите артефакти във възстановените снимки и до колко са дразнещи. За математическа оценка намерете средната квадратична сума от разликите за всеки пиксел от възстановената и оригиналната снимка.
, където
- n - броя пиксели по височина
- m - броя пиксели по дължина
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{n,m} = O_{n,m} - R_{n,m} }
- On,m - пиксел от оригиналното изображение
- Рn,m - пиксел от възстановеното изображение
Контролни въпроси и задачи
- Каква е разликата между CMOS и CCD сензорите?
- Защо филтрите на зеления цвят са два пъти повече от тези на червения и на синия?
- Кога е удачно да се използва интерполация nearest neighbor и кога бикубична интерполация ?
Matlab
Основни функции за работа с изображения:
- imread('file_name') - зареждане на изображение от файл. Ако е цветно избражението ще се зареди в масив (матрица) с размери n*m*3, където n и m са размерите на изображението;
- imshow(img) - визуализиране на изображение;
- imwrite(img,'file_name') - запис на избражение във файл;
червен канал
lena = imread('/home/ilianko/ram/lena_std.tif');
lena(:,:,3) = 0; %Нулиране на всички елементи от третото изерение
lena(:,:,2) = 0; %Нулиране на всички елементи от второ измерение
RAW = lena(:,:,1); %Визулизиране на първо измерение
imwrite(lena, 'R.tif');
imwrite(RAW, 'BW.tif');
imshow(RAW);
Bayer pattern
lena = imread('/home/ilianko/ram/lena_std.tif');
RAW = uint8(zeros(512));
for x = 1:2:511
for y = 1:2:511
RAW(x,y) = lena(x,y,1); % red
RAW(x+1,y) = lena(x+1,y,2); % green
RAW(x,y+1) = lena(x,y+1,2); % green
RAW(x+1,y+1) = lena(x+1,y+1,3); % blue
end
end
imwrite(RAW, 'test.tif');
imshow(RAW);
Nearest Neighbor
lena = imread('/home/ilianko/ram/test.tif');
RGB = uint8(zeros(512:512:3));
for x = 1:2:511
for y = 1:2:511
RGB(x,y,1) = lena(x,y); % red
RGB(x+1,y+1,1) = lena(x,y); % red
RGB(x+1,y,1) = lena(x,y); % red
RGB(x,y+1,1) = lena(x,y); % red
RGB(x,y,2) = lena(x+1,y); % green
RGB(x+1,y+1,2) = lena(x,y+1); % green
RGB(x+1,y,2) = lena(x+1,y); % green
RGB(x,y+1,2) = lena(x,y+1); % green
RGB(x,y,3) = lena(x+1,y+1); % blue
RGB(x+1,y+1,3) = lena(x+1,y+1); % blue
RGB(x+1,y,3) = lena(x+1,y+1); % blue
RGB(x,y+1,3) = lena(x+1,y+1); % blue
end
end
imwrite(RGB, 'testN.tif');
imshow(RGB);
Bilinier
lena = imread('/home/ilianko/ram/test.tif');
%RGB(1:512,1:512,1:3) = uint8(128);
for x = 3:2:509
for y = 3:2:509
RGB(x,y,1) = lena(x,y); % red
RGB(x,y+1,1) = (lena(x,y)/2+lena(x,y+2)/2); % red
RGB(x+1,y,1) = (lena(x,y)/2+lena(x+2,y)/2); % red
RGB(x+1,y+1,1) = (lena(x,y)/4+lena(x+2,y)/4+lena(x,y+2)/4+lena(x+2,y+2)/4); % red
RGB(x,y,2) = (lena(x-1,y)/4+lena(x+1,y)/4+lena(x,y-1)/4+lena(x,y+1)/4); % green
RGB(x+1,y+1,2) = (lena(x+1,y)/4+lena(x+1,y+2)/4+lena(x,y+1)/4+lena(x+2,y+1)/4); % green
RGB(x+1,y,2) = lena(x+1,y); % green
RGB(x,y+1,2) = lena(x,y+1); % green
RGB(x,y,3) = (lena(x+1,y+1)/4+lena(x-1,y-1)/4+lena(x+1,y-1)/4+lena(x-1,y+1)/4); % blue
RGB(x+1,y+1,3) = lena(x+1,y+1); % blue
RGB(x+1,y,3) = (lena(x+1,y+1)/2+lena(x+1,y-1)/2); % blue
RGB(x,y+1,3) = (lena(x+1,y+1)/2+lena(x-1,y+1)/2); % blue
end
end
imwrite(RGB, 'testNNS.tif');
imshow(RGB);
Инсталация openCV
1. Инсталирайте cmake sudo apt-get install cmake
2. Инсталирайте библиотеката libgtk2.0-dev
sudo apt-get install libgtk2.0-dev
3. да се свали openCV 2.2 и разархивирайте в директория Downloads/OpenCV-2.2.0
4. Влезте в директорията
cd Downloads/OpenCV-2.2.0 cmake -D CMAKE_BUILD_TYPE=RELEASE -D CMAKE_INSTALL_PREFIX=/usr/local ./ make make install
export LD_LIBRARY_PATH=/home/lab/Downloads/OpenCV-2.2.0/lib:$LD_LIBRARY_PATH sudo ldconfig
Следните опции се добавят при компилиране: -lopencv_core -lopencv_imgproc -lopencv_calib3d -lopencv_video -lopencv_features2d -lopencv_ml -lopencv_highgui -lopencv_objdetect -lopencv_contrib -lopencv_legacy
1. Разглежда не R, G, B каналите
#include <opencv/highgui.h> //OpenCV GUI functions ̄include <stdio.h>
#include <opencv/cv.h> //main OpenCV functions
int main()
{
IplImage *img, *img_r, *img_g, *img_b ; // image structer
int x,y, w = 512, h = 512; //image size
img_r = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 1 );
img_g = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 1 );
img_b = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 1 );
img = cvLoadImage("lena_std.tif",1);
for(x=0; x<img->width; x++)
{
for(y=0;y<img->height; y++)
{
(img_r->imageData + img_r->widthStep*y)[x]= (img->imageData + img->widthStep*y)[x*3+2];
(img_g->imageData + img_g->widthStep*y)[x]= (img->imageData + img->widthStep*y)[x*3+1];
(img_b->imageData + img_b->widthStep*y)[x]= (img->imageData + img->widthStep*y)[x*3];
}
}
cvNamedWindow("red", 1);
//display the image in the window
cvShowImage("red", img_r);
cvNamedWindow("green", 1);
//display the image in the window
cvShowImage("green", img_g);
cvNamedWindow("blue", 1);
//display the image in the window
cvShowImage("blue", img_b);
cvNamedWindow("rgb", 1);
//display the image in the window
cvShowImage("rgb", img);
//wait for key to close the window
cvWaitKey(0);
cvDestroyWindow( "blue" ); //destroy the window
cvDestroyWindow( "red" );
cvDestroyWindow( "green" );
cvDestroyWindow( "rgb" );
cvReleaseImage( &img ); //release the memory for the image
cvReleaseImage( &img_r );
cvReleaseImage( &img_g );
cvReleaseImage( &img_b );
return 0;
}
2. Получаване на черно бяло изображение
include <opencv/highgui.h> //OpenCV GUI functions ̄include <stdio.h>
#include <opencv/cv.h> //main OpenCV functions
int main()
{
IplImage *img, *img_bw ; // image structure
int x,y, w = 512, h = 512; //image size
img_bw = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 1 );
img = cvLoadImage("lena_std.tif",1);
for(x=0; x<img->width; x++)
{
for(y=0;y<img->height; y++)
{
(img_bw->imageData + img_bw->widthStep*y)[x] =
((uchar)((img->imageData + img->widthStep*y)[x*3+2]) >> 2 ) + ((uchar)((img->imageData + img->widthStep*y)[x*3+2]) >> 4 ) +
((uchar)((img->imageData + img->widthStep*y)[x*3+1]) >> 1 ) + ((uchar)((img->imageData + img->widthStep*y)[x*3+1]) >> 4 ) +
((uchar)((img->imageData + img->widthStep*y)[x*3]) >> 3 );
}
}
cvNamedWindow("rgb", 1);
//display the image in the window
cvShowImage("rgb", img);
cvNamedWindow("bw", 1);
//display the image in the window
cvShowImage("bw", img_bw);
//wait for key to close the window
cvWaitKey(0);
cvDestroyWindow( "bw" );
cvDestroyWindow( "rgb" );
cvReleaseImage( &img ); //release the memory for the image
cvReleaseImage( &img_bw );
return 0;
}
3. Извличане на Bayer pattern
#include <opencv/highgui.h> //OpenCV GUI functions ̄include <stdio.h>
#include <opencv/cv.h> //main OpenCV functions
int main()
{
IplImage *img, *img_bw ; // image structure
int x,y, w = 512, h = 512; //image size
img_bw = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 1 );
img = cvLoadImage("lena_std.tif",1);
int b = 1, r = 0, g = 1, br = 0;
for(x=0; x<img->width; x++)
{
b = ( b == 1 ) ? 0 : 1;
r = ( r == 1) ? 0 : 1;
for(y=0;y<img->height; y++)
{
g = (g == 1) ? 0 : 1;
br = (br == 1) ? 0 : 1;
(img_bw->imageData + img_bw->widthStep*y)[x] =
((uchar)((img->imageData + img->widthStep*y)[x*3+2])*br*r)+
((uchar)((img->imageData + img->widthStep*y)[x*3+1])*br*b) + ((uchar)((img->imageData + img->widthStep*y)[x*3+1])*g*r)+
((uchar)((img->imageData + img->widthStep*y)[x*3])*g*b);
}
}
cvNamedWindow("rgb", 1);
//display the image in the window
cvShowImage("rgb", img);
cvNamedWindow("bw", 1);
//display the image in the window
cvShowImage("bw", img_bw);
cvSaveImage("raw.bmp", img_bw, 0);
//wait for key to close the window
cvWaitKey(0);
cvDestroyWindow( "bw" );
cvDestroyWindow( "rgb" );
cvReleaseImage( &img ); //release the memory for the image
cvReleaseImage( &img_bw );
return 0;
}
4. Преобразуване от bayer pattern в RGB
#include <opencv/highgui.h> //OpenCV GUI functions ̄include <stdio.h>
#include <opencv/cv.h> //main OpenCV functions
int main()
{
IplImage *img, *img_bw ; // image structure
int x,y, w = 512, h = 512; //image size
img = cvCreateImage( cvSize( w, h ), IPL_DEPTH_8U, 3 );
img_bw = cvLoadImage("raw.bmp",0);
int b = 0, r = 1, g = 1, br = 0;
for(x=1; x<img->width-1; x++)
{
b = ( b == 1 ) ? 0 : 1;
r = ( r == 1) ? 0 : 1;
for(y=1;y<img->height-1; y++)
{
g = (g == 1) ? 0 : 1;
br = (br == 1) ? 0 : 1;
(img->imageData + img->widthStep*y)[x*3] = (img_bw->imageData + img_bw->widthStep*(y-1*g))[x-1*r];
(img->imageData + img->widthStep*y)[x*3+1] = (img_bw->imageData + img_bw->widthStep*(y+1*br))[x]*b +
(img_bw->imageData + img_bw->widthStep*(y+1*g))[x]*r;
(img->imageData + img->widthStep*y)[x*3+2] = (img_bw->imageData + img_bw->widthStep*(y+1*br))[x+1*b] ;
}
}
cvNamedWindow("rgb", 1);
//display the image in the window
cvShowImage("rgb", img);
cvNamedWindow("bw", 1);
//display the image in the window
cvShowImage("bw", img_bw);
cvSaveImage("out1.bmp", img, 0);
//wait for key to close the window
cvWaitKey(0);
cvDestroyWindow( "bw" );
cvDestroyWindow( "rgb" );
cvReleaseImage( &img ); //release the memory for the image
cvReleaseImage( &img_bw );
return 0;
}
5. Оценка на разликите