Махало

Движение на махало под въздействие на гравитацията

Цел: Създаване на връзки между диференциране и диференциални уравнения.

Постановка: Математическо махало. (Съпротивлението на въздуха се пренебрегва). Да се намери зависимостта на махалото спрямо времето, т.е. функцията на движение на махалато.

Анализ: Във всеки момент махалото се движи с различна скорост и ускорение, зависещи от ъгъла на отклонение на махалото.

Производни, разстояние, скорост и ускорение.

Движението на махалото се извършва по окръжност с радиус равен на дължината на нишката, на която е окачено махалото. От тук, следва че:

$s=\ell \theta$

За да изразим скоростта ползваме първата производна (изменението на разстоянието за единица време). Изменя се само ъгълът, а дължината на нишката е константа и се запазва:

$v={ds \over dt}={{d\ell \theta } \over dt}=\ell {d\theta \over dt}$

По да изразим ускорението, използваме втората производна

$a={d^{2}s \over dt^{2}}=\ell {d^{2}\theta \over dt^{2}}$ (1)

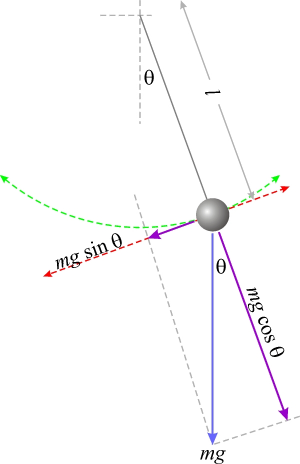
Сили действащи на махалото

Под внимание се взема само силата действаща по посока на движението. Допирателната по окръжността на движение (тангенциалната сила ( танго -> допир)). Перпендикулярната сила (нормалната ) се неутрализира.

От II закон на нютон $F=ma\,$

За махалото $F=gm\sin \theta =-ma\,=>a=-g\sin \theta \,$ (2)

Диференциално уравнение на махало

От (1) и (2) $=>-g\sin \theta =\ell {d^{2}\theta \over dt^{2}}<=>\ell {d^{2}\theta \over dt^{2}}+g\sin \theta =0$

Решаване на диференциалното уравнение

Има два подхода при решаване на диференциални уравнения, аналитичен и числен. При конкретното уравнение са възможни и двата подхода, но аналитичният метод може да се използва за $\theta <20^{\circ }$. В този случай диференциалното уравнение ще се преобразува в линейно от втори ред.

Аналитично решение

$\ell {d^{2}\theta \over dt^{2}}+g\sin \theta =0<=>\ell {d^{2}\theta \over dt^{2}}+g\theta =0,\theta <20^{\circ }$

Полагаме $\ {\theta }={y}$, от тук $\ell {y''}+{g}{y}=0$ - хомогенно диференциално уравнение от 2-ри ред

Уравнението е от вида $\ ay''+by'+cy=0$, затова лесно могат да се намерят решения във вида $\ y=c_{1}e^{r_{1}x}+c_{2}e^{r_{2}x}$, където за r се решава уравнението $\ ar^{2}+br+c=0$, a именно:

$\ell r^{2}+g=0$

$r=\pm j{\sqrt {\frac {g}{l}}}$

$\ y(t)=c_{1}e^{-j{\sqrt {\frac {g}{l}}}t}+c_{2}e^{j{\sqrt {\frac {g}{l}}}t}$

$\ e^{jx}=cos(x)+jsin(x)$ от тук =>

$\ \theta (t)=C_{1}cos({\sqrt {\frac {g}{l}}}t)+C_{2}sin({\sqrt {\frac {g}{l}}}t)$

За получаване на конкретно решение ще зададем начални условия. Примерно в началното положение $\ t=0$, махалото е отклонено на $\ \theta _{0}$ градуса и пуснато свободно, т.е. с нулева начална скорост.

${\begin{cases}\theta (0)=\theta _{0}=C_{1}cos({\sqrt {\frac {g}{l}}}0)+C_{2}sin({\sqrt {\frac {g}{l}}}0)\\\theta (0)'=0=-C_{1}{\sqrt {\frac {g}{l}}}sin({\sqrt {\frac {g}{l}}}0)+C_{2}{\sqrt {\frac {g}{l}}}cos({\sqrt {\frac {g}{l}}}0)\end{cases}}$ => $\ C_{1}=\theta _{0},C_{2}=0$

За решение на задача при малки ъгли се получава

$\theta (t)=\theta _{0}cos({\sqrt {\frac {g}{l}}}t)$

${\sqrt {\frac {g}{l}}}={\sqrt {{\frac {m}{s^{2}}}*{\frac {1}{m}}}}={\frac {1}{s}}=\omega *{\frac {rad}{s}}$ e ъгловата скорост с която ще се движи махалото.

От тук $\ \theta (t)=\theta _{0}cos(\omega t)$

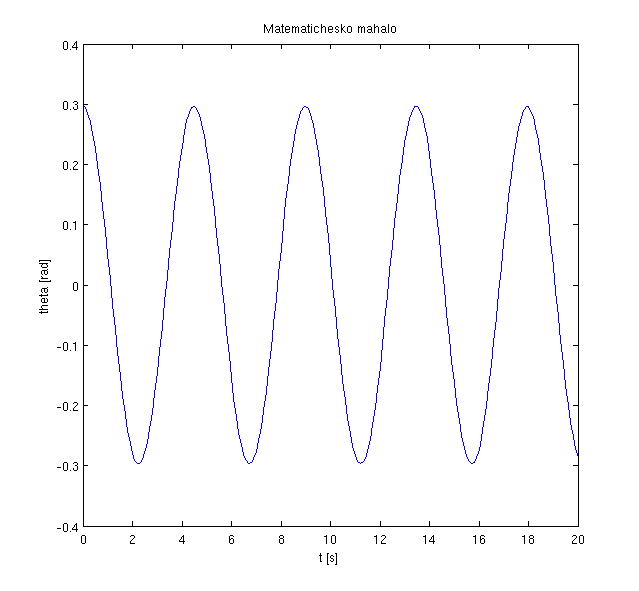
Визуализация на решението с матлаб

Имаме следните начални условия:

• $\ l=5*m$
• $\theta _{0}=17^{\circ }$

l = 5; % m
g = 9.8; % m/s^2
theta_0 = 17; % degree
theta_0r = 17*pi/180 % ъгъл в радиани
omega = sqrt(g/l); % ъгловата скорост
t = 0:0.1:20; % интуитивно си избираме подходящ интервал за изследване
theta = theta_0r*cos(omega.*t); % Фундаментална формула, с който започва анализа на трептенията

% За тези с по-малко въображение и тези, които искат да представят резултатите на други
plot(t,theta); 
xlabel('t [s]'), ylabel('theta [rad]');
axis([ 0 20 -0.4 0.4]);
title('Matematichesko mahalo');
% Само трябва да добавим съпротивление на въздуха; вятър; маса на нишката, която държи махалото; трептене на опрната точка и да решим за всякакви начални условия. 

Нито повече, нито по-малко от една синосоида