Махало

Движение на махало под въздействие на гравитацията

Цел: Създаване на връзки между диференциране и диференциални уравнения.

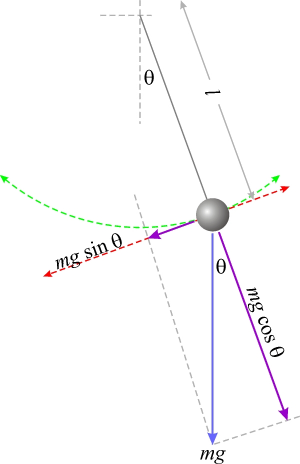
Постановка: Математическо махало. ( Съпротивлението на въздуха се пренебрегва).

Производни, разстояние, скорост и ускорение.

Движението на махалото се извършва по окръжност с радиус равен на дължината на нишката, на която е окачено махалото. От тук, следва че:

$s=\ell \theta$

За да изразим скоростта ползваме първата производна (изменението на разстоянието за единица време):

Failed to parse (unknown function "\dt"): {\displaystyle v = {ds\over dt} = {{d\ell\theta}\over dt} = \ell {d\theta\over\dt}}

Изминатото разстояние на махалото може да намерим