Difference between revisions of "Изкуствени невронни мрежи"
| (3 intermediate revisions by the same user not shown) | |||
| Line 30: | Line 30: | ||
[[Image:neuron.png]] | [[Image:neuron.png]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Основни елементи на невронните мрежи == | ==Основни елементи на невронните мрежи == | ||
| Line 65: | Line 50: | ||
Обикновено предавателната функция е [[ненамаляваща функция]] на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция. | Обикновено предавателната функция е [[ненамаляваща функция]] на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция. | ||
| + | |||
| + | Има три най-често използвани функции за активиране на неврон. Oзначаваме с <math>u = \sum_{j}{w_{ij}x_j} </math> сумарният вход | ||
| + | *Активация с гранична стойност | ||
| + | <math> x_i = \left\{\begin{matrix} 1 & \mbox {if } u >\theta_i, \\ | ||
| + | 0 & \mbox {otherwise.}\end{matrix}\right.</math> | ||
| + | *Активация със скачаща функция | ||
| + | <math> x_i = max \left \{ 0, min \left \{ 1, x+0.5 \right \} \right \}</math> | ||
| + | *Активация със сигмоидална функция | ||
| + | <math> x_i = \frac{a}{1+e^{-bu}} </math> | ||
| + | **a - усилване, амплитуда на предавателната функция | ||
| + | **b - наклон на предавателната функция | ||
==Мрежови архитектури== | ==Мрежови архитектури== | ||
Latest revision as of 13:22, 11 January 2013
Contents
Какво е невронна мрежа
Изкуствена невронна мрежа е математически модел, съставен от набор отделни елементи, които имитират:
- свойства на биологични невронни системи;
- процесите на адаптивно биологично усвояване на нови знания и умения.
При решаване на задачи като:
- разпознаване на говор,
- разпознаване на образи,
- разпознаване по образец и т.н.,
се счита, че невронните мрежи могат да се прилагат успешно.
Съвременният модел на невронна мрежа е композиция на добре взаимодействащи си елементи (аналог на невроните) и свързващите ги канали (аналог на синапсите).
Основно свойство на невронните мрежи е самообучението (само-модификацията).
Човешкият мозък притежава изчислителни свойства, които се доста уникални. Тези свойства сериозно се различават от свойствата на дигиталния компютър. Началото на ИНМ се поставя с изследване на изчислителните следствия на тези различия.
Това води до разработването на нов подход при обработка на данни в изкуствения интелект, вдъхновен от начина, по който това се извършва в човешкия мозък.
Невронните мрежи изучават и прилагат:
- подробни и правдиви модели за реални мозъчни структури;
- висшите и абстрактни свойства на невронни изчисления.
Неврони
http://bg.wikipedia.org/wiki/Неврон
Основни елементи на невронните мрежи
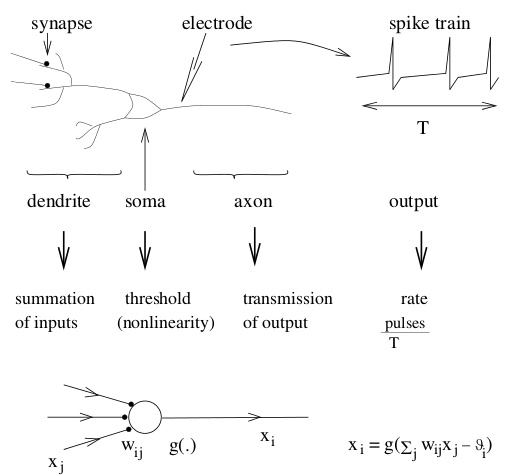
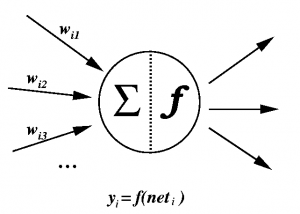
Основният обработващ елемент в изкуствените невронни мрежи е изкуственият неврон. Той не съответства напълно на биологичните неврони. На фигурата по-долу е представен изкуствен неврон.
Всеки неврон получава входен сигнал от съседни неврони или други източници и го използва, за да изчисли изходен сигнал, който предава на други възли в мрежата. Различават се три типа възли в невронната мрежа:
- входни възли, които получават данни от средата, в която работи системата;
- изходни възли, които изпращат данни навън от системата;
- скрити възли, чиито входни и изходни сигнали са в мрежата.
Обработката на информацията, която се извършва от неврона може да се представи със следния израз:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {y_i}=f \left( \sum_{j}{w_{ij}}{y_j} \right) }
,
където i е индекс на неврона. С wij е означен тегловният коефициент на връзката между тялото на j неврона (синапсиса) и дендритите на i-ия неврон. С yj е означена активността на невроните, свързани с неврон i, yi е изходът на неврона, f е предавателна функция.
Ако стойността на теглото wij е положителна, връзката е възбуждаща, в противен случай е подтискаща.
Обикновено предавателната функция е ненамаляваща функция на тоталния вход на даден неврон. Най-често се използва линейна, полулинейна или сигмоидална функция.
Има три най-често използвани функции за активиране на неврон. Oзначаваме с Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \sum_{j}{w_{ij}x_j} } сумарният вход
- Активация с гранична стойност
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i = \left\{\begin{matrix} 1 & \mbox {if } u >\theta_i, \\ 0 & \mbox {otherwise.}\end{matrix}\right.}
- Активация със скачаща функция
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i = max \left \{ 0, min \left \{ 1, x+0.5 \right \} \right \}}
- Активация със сигмоидална функция
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i = \frac{a}{1+e^{-bu}} }
- a - усилване, амплитуда на предавателната функция
- b - наклон на предавателната функция
Мрежови архитектури
В зависимост от вида на връзките между невроните мрежите са:
- прави мрежи - данните се предават от входните към изходните възли без обратни връзки. Мрежата може да бъде от един или няколко слоя;
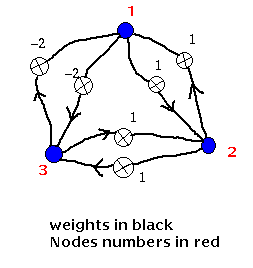
- рекурсивни мрежи - има и обратни връзки. Динамичните свойства на тези мрежи са важни. При обучение невроните са с неопределена активност, която се променя докато мрежата достигне състояние, в което не настъпват повече значителни промени. В рекурсивните мрежи няма разлика между вход и изход, по-скоро има набор от видими неврони, които комуникират със средата и набор от скрити неврони, които нямат подобна функция.
Класически пример за права мрежа е перцептронът.
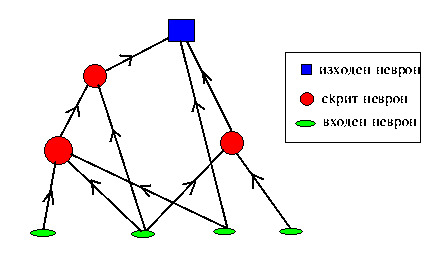
Типична рекурсивна мрежа е дадена на фигурата по-долу.
Обучение на невронни мрежи
Според вида на управление обучението бива:
- обучение с учител или асоциативно обучение, при което на мрежата се предоставят входният и съответният му изходен образец. Обучаващите входно-изходни двойки се предоставят от учител или от системата, включваща мрежата. Теглата се уточняват като се се използва разликата между стойностите на изходните неврони при зададен входен образец и стойностите на тези възли, които трябва да се получат при коректна работа на мрежата.
- обучение без учител или самоорганизация, при което изходните неврони се обучават да отговарят на набори от входни образци. Предварително няма множество от категории, към които да се класифицират входните образци. Системата сама открива най-характерните черти на входните набори и изработва свое собствено представяне на входните стимули.
Обучението на невронните мрежи се извършва по алгоритъм, включващ правило, което модифицира теглата на връзките между невроните. Съществуват две правила, които могат да се модифицират за обучение на различни мрежи:
- правило на Хеб - теглото на връзката между неврони i и j, където неврон i получава вход от неврон j, се увеличава пропорционално на произведението от активностите на неврони i и j.
При обучение с p наброй входни модела Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{ij} = \frac{1}{p} \sum_{k=1}^p x_i^k x_j^k\,}
- правило на Уидроу-Хоф или делта правило - теглото на връзката между неврони i и j, където неврон i получава вход от неврон j, се увеличава пропорционално на произведението от разликата на желаната и действителната активност на неврон i и активността на неврон j.
Видове мрежи
Мрежи на Хопфийлд
В модела на Хопфийлд всеки неврон е свързан с всеки друг неврон. Потокът от информация в тази мрежа не е в едно направление. Възможно е информацията от възел да се върне през други възли към същия възел. Това означава, че мрежата е с обратна връзка и се нарича още рекурсивна мрежа.
Коефициентите на тегловните връзки се описват с: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {W_{ij}}= \frac{1}{N} \sum_{m=1}^p{X^m_i}{X_j^m}}
където N е броя невроните, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^m_j} е стойността на неврон j в набор m.
Обучението е с правилото на Хеб. Обучаващото правило работи добре, когато наборите, които трябва да се записват са произволни с еднаква вероятност за (+1) и (-1). В големи мрежи (N клони към безкрайност) броят сучайни набори, които могат да се запазват е приблизително 0.14 по N.
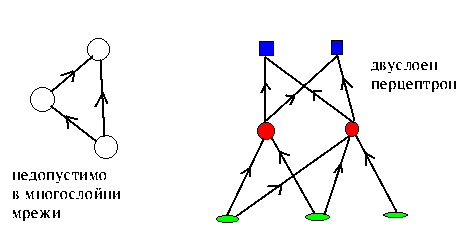
Обикновени перцептрони
Многослойните прави мрежи са наречени перцептрони, когато за първи път са били изучавани от Розенблат. Фигурата показва пример на двуслоен перцептрон.
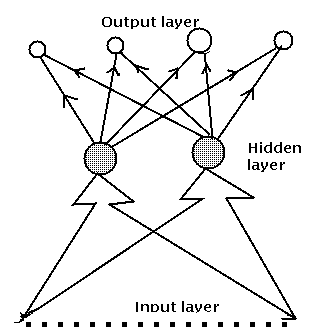
Правите многослойни мрежи или т.нар. перцептрони имат входни възли, които предават входния образец към останалата част от мрежата. Следват един или няколко междинни слоя от неврони, които нямат пряка връзка с външната среда и обикновено се наричат скрити. В изходния слой се чете резултатът от изчисленията.
Правите мрежи имат асиметрични матрици на теглата wij, всички връзки са еднопосочни.
Правите еднослойни мрежи се наричат обикновени перцептрони. Те нямат скрити слоеве. Ако с xk и yi означим съответно входовете и изходите, то изчисленията в такива мрежи могат да се опишат с: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_i = g\left( \sum_{k}{w_{ik} x_k} \right)} , където сумирането е по k, а g е функцията, чрез която невроните изчисляват стойностите на активностите си. Обикновено тази функция се избира нелинейна - може да се използва прагова, синоидална или друга. Изходът винаги е явна функция на входа.
Общият вид на задачата при тези мрежи е търсене на предварително зададен изходен образец в отговор на входен образец.
Входните, изходните и желаните стойности могат да бъдат булеви или непрекъснати.
Ако съществува множество от тегла, които да извършват необходимите изчисления, то те могат да бъдат открити с просто обучаващо правило. То започва със случайно предложение за теглата, след което се правят подобрения. Решението се намира след краен брой стъпки.
Многослойни мрежи
Многослойните прави мрежи сe обучават с алгоритъм за обратно разпространяване на грешката:
Алгоритъмът за обратно разпространение на грешката и негови варианти се прилагат за решаване на различни задачи.
Представяне на логическата функция XOR
Четност
Задача за кодирането Намира се ефективно множество от образци, представени чрез скритите неврони, които кодират голям брой входно/изходни образци. Броят на скритите неврони е малък, за да се получи ефективно кодиране.
- Net Talk
- Разпознаване на сигнали от локатор
- Управление на кола
- Компресия на изображения
- Разпознаване на реч
Правите мрежи се използват най-често за разграничаване на множество от думи. На входа на мрежата се подава представяне на произнесена дума и перцептронът се обучава да я разпознава. На практика това е приложимо към задачи с малък речник и отделни думи.
Мaшини на Болцман
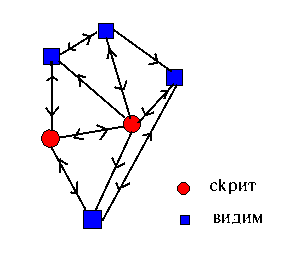
Машините на Болцман могат да се разглеждат като разширение на мрежите на Хопфийлд, които включват скрити неврони. Невроните се разделят на видими и скрити. Видимите могат, но не е задължително да бъдат разделени на входни и изходни възли. Скритите възли нямат връзка с външната среда. Връзките между невроните могат да бъдат пълни - между всяка двойка - или структурирани по друг начин. Всички връзки трябва да бъдат симетрични, т.е. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{ij} = w_{ji}} . Невроните са стохастични и приемат изходни стойности Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i = +1} с вероятност Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(h_i)} и Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i=-1} с вероятност Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - g(h_i)} .
Мрежата се нарича машина на Болцман, защото вероятностите за отделните състояния на системата се дават чрез болцмановото разпределение от статистическата механика.
Обучението за машина на Болцман е обучение с учител, но може да се използва и като самообучение. Обучението се състои в увеличаване на теглата на връзките между неврони, които са склонни да бъдат активни едновременно ( правило на Хеб). Този подход се реализира, като се използват статистически изчисления.
В оригиналната си форма обучаващият алгоритъм на Болцман е много бавен и затова са правени по-малко приложения в сравнение с back-propagation.
Машините на Болцман са прилагани към редица проблеми сред които са: компютърно зрение, статистическо разпознаване на образи, разпознаване на реч и комбинаторни оптимизационни проблеми. Въпреки че са бавни, те са ефективни и постигат значително по-голяма точност в сравнение с back-propagation.
Самообучаващи се мрежи
Самообучаващите се архитектури са най-често доста прости. Повечето мрежи се състоят от един слой. Обикновено са прави, а изходите са много по-малко от входовете. Тези архитектури са най-близки до невробиологичните.
Обучението на този вид мрежи е без учител, т.е. мрежата сама трябва да открие образци, характеристики, регулярности, корелации или категории във входните данни и да ги кодира на изхода. За да се получи това невроните и връзките трябва да показват някаква степен на самоорганизация.
Самообучението може да се реализира само при изобилие от входни данни. Типът на образеца, който самообучаващата мрежа открива във входните данни зависи от архитектурата. Подобна мрежа предоставя описаните по-долу възможности.
- Прилика - един неврон с непрекъсната стойност на активност може да покаже колко подобен е новият входен образец на типични или усреднени образци, представени преди това.
- Принципен компонентен анализ - аналогични на гореописания случай, с няколко неврона се измерва подобие с предишни примери.
- Кластеризация - множество от двоични изходи, само един от които е активен в даден момен време, определят към коя от няколко категории принадлежи входният образец.
- Определяне на прототип - мрежата формира категории като в предишния случай и дава като изход един екземпляр - прототип на съответния клас.
- Кодиране - изходът може да е кодирана версия на входа. Използва се за компресиране на данни преди предаването им по канал, като се конструира и обратна декодираща мрежа.
- Картографиране на характеристики - изходните неврони имат фиксирана геометрична структура и само един е активен в даден момент от време, те могат да изобразяват входните образци в различни точки от тази структура.
Хардуерна реализация
Невронните мрежи се изработват като чипове, които могат да бъдат аналогови, цифрови или хибридни.
Аналоговите хардуерни решения на невронни мрежи са комбинация от линейни и нелинейни устройства. Основен компонент е транзисторът. Срещат се кондензатори и резистори. Основният им недостатък е липсата на термична стабилност.
Цифровите невронни чипове са изградени от RAM памети, цифрови суматори и умножители и цифрови схеми за реализация на предавателната функция. Паметите съхраняват теглата на връзките. Едно от основните им предимства е високата шумоустойчивост.
Хибридните невронни чипове комбинират цифров и аналогов подход за постигане на най-добри качества на чипа. Например може да се комбинира цифрова памет с цифрови или двоични умножители, а сумирането е предавателната функция да се реализират аналогово.
Приложения на невронните мрежи
Невронни мрежи в практиката
Тъй като невронните мрежи са най-подходящи за идентифициране на схеми и тенденции в данни, те са подходящи за приложения, свързани с:
- прогнозиране на продажби
- контрол на индустриални процеси;
- проучвания на потреблението;
- валидизиране на данни;
- финансов анализ.
- планиране и оптимизация.
- управление на риска.
Невронни мрежи в медицината
Изследванията са насочени към моделиране на части от човешкото тяло и разпознаване на болести от различни изображения - от компютърна томографиия, ултразвукови сканирания и кардиограми...
Тъй като невронните мрежи се обучават от примери не са нужни специални алгоритми за разпознаване на заболяванията. Достатъчен е набор от примери, който е представителен за даденото заболяване.
Моделиране и диагностика на сърдечно-съдовата система. Невронни мрежи са използвани експериментално за моделиране на сърдечно-съдовата система. Разработеният индивидуален модел може да се сравнява с реалните физиологически измервания на пациента, за да се постави диагноза.
Невронните мрежи са в състояние да комбинират сигнали от различни сензори. Могат да заучават сложни взаимоотношения между стойности от различни сензори.
Невронни мрежи се използват за създаване на електронен нос, който регистрира миризми с приложение в телехирургия.
Връзки
http://lcn.epfl.ch/tutorial/english/