Difference between revisions of "Упражнение 5. Matlab"
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Стринг с апостроф == | == Стринг с апостроф == | ||
| − | Когато искаме апостроф слагаме два апострофа | + | <span style="red">Когато искаме апостроф слагаме два апострофа!</span> |
<pre>ilian'co => ilian''co</pre> | <pre>ilian'co => ilian''co</pre> | ||
| − | = | + | <pre> |
| + | >> ''diff'' | ||
| + | ??? ''diff'' | ||
| + | | | ||
| + | Error: Unexpected MATLAB expression. | ||
| + | |||
| + | >> '''diff''' | ||
| + | ans = | ||
| + | 'diff' | ||
| + | </pre> | ||
| + | == Масив от клетки == | ||
| + | Всеки елемент може да е от различен тип | ||
| + | |||
| + | <code><pre> | ||
| + | Cells = { 10, pi, 3+4i, 'MuPad', [1 2 3], [1 2 3; 4 5 6] , {'a', 1} } | ||
| + | |||
| + | Cells = | ||
| + | |||
| + | Columns 1 through 5 | ||
| + | |||
| + | [10] [3.1416] [3.0000 + 4.0000i] 'MuPad' [1x3 double] | ||
| + | |||
| + | Columns 6 through 7 | ||
| + | |||
| + | [2x3 double] {1x2 cell} | ||
| + | </pre></code> | ||
| + | |||
| + | Достъп до всички данни на масива от клетки | ||
| + | for i = 1:6, Cells(i), end | ||
| + | Cells{6}{2} | ||
| + | |||
| + | == Преобразувания на Лаплас == | ||
| + | <code><pre> | ||
| + | >> syms h w p k | ||
| + | >> syms t, ilaplace(h*w/((p^2+w^2)*(p^2+k^2)), p, t) | ||
| + | |||
| + | ans = | ||
| + | |||
| + | (h*sin(t*w))/((k + w)*(k - w)) - (h*w*sin(k*t))/(k*(k + w)*(k - w)) | ||
| + | |||
| + | >> y = simplify(ans) | ||
| + | |||
| + | y = | ||
| + | |||
| + | (h*(k*sin(t*w) - w*sin(k*t)))/(k*(k^2 - w^2)) | ||
| + | |||
| + | >> pretty(y) | ||
| + | |||
| + | h (k sin(t w) - w sin(k t)) | ||
| + | --------------------------- | ||
| + | 2 2 | ||
| + | k (k - w ) | ||
| + | >> | ||
| + | </pre></code> | ||
| + | |||
| + | syms p x, fi = ilaplace(1/(p-1)^2, p, x) | ||
| + | fi = | ||
| + | x*exp(x) | ||
| + | |||
| + | <code><pre> | ||
| + | |||
| + | >> syms x p k w | ||
| + | >> f = exp(-k*x)*sin(w*x + k); | ||
| + | >> F = laplace(f, x, p) | ||
| + | |||
| + | F = | ||
| + | |||
| + | (sin(k)*(k + p) + w*cos(k))/((k + p)^2 + w^2) | ||
| + | |||
| + | >> syms t, pretty(simplify(F, p,x)) | ||
| + | ??? Error using ==> sym.simplify | ||
| + | Too many input arguments. | ||
| + | |||
| + | >> syms t, simplify(ilaplace(F, p,x)) | ||
| + | |||
| + | |||
| + | |||
| + | ans = | ||
| + | |||
| + | sin(k + w*x)/exp(k*x)</pre></code> | ||
| + | |||
| + | Пример: ... няма го | ||
| + | |||
| + | >> syms x p ,laplace(exp(-x)*sin(2*x),x,p) | ||
| + | ans = | ||
| + | 2/((p + 1)^2 + 4) | ||
| + | |||
| + | y = ilaplace(2*p/((p^2+p+1)*((p+1)^2+4)), p, x) | ||
| + | plot(-13:0.01:3,subs(y,x, -13:0.01:3)) | ||
| + | [[Image:LPlot.png|frame|none|Лаплас]] | ||
| + | |||
| + | Проверка | ||
| + | >> diff(y,x) +y + int(subs(y,x,t),t,0,x) | ||
| + | ans = | ||
| + | (2*cos(2*x))/(13*exp(x)) - (8*(cos(2*x)/4 - 2*sin(2*x)))/(13*exp(x)) - (8*(cos((3^(1/2)*x)/2)/4 + | ||
| + | (3^(1/2)*sin((3^(1/2)*x)/2))/2))/(13*exp(x/2)) - (2*cos((3^(1/2)*x)/2))/(13*exp(x/2)) - | ||
| + | (3*sin(2*x))/(13*exp(x)) + (4*(cos((3^(1/2)*x)/2) - (3^(1/2)*sin((3^(1/2)*x)/2))/6))/(13*exp(x/2)) + | ||
| + | (14*3^(1/2)*sin((3^(1/2)*x)/2))/(39*exp(x/2)) | ||
| + | >> simplify(ans) | ||
| + | ans = | ||
| + | sin(2*x)/exp(x) | ||
| + | |||
| + | |||
| + | |||
| + | == Решаване системи линейни уравнения == | ||
| + | |||
| + | A*x= B | ||
| + | x = A\B % \ може да се прилага при правоъгълни матрици, при повече редове от колони се решава за средно квадратичната стойност | ||
| + | |||
| + | A = [3 7 5; 2 6 9; 4 4 4] | ||
| + | A = | ||
| + | |||
| + | 3 7 5 | ||
| + | 2 6 9 | ||
| + | 4 4 4 | ||
| + | >> b = [2 3 4]' | ||
| + | b = | ||
| + | 2 | ||
| + | 3 | ||
| + | 4 | ||
| + | >> A\b | ||
| + | ans = | ||
| + | 1.0500 | ||
| + | -0.4500 | ||
| + | 0.4000 | ||
| + | |||
| + | При лошо обоснована матрица може да има грешки | ||
| + | >> A = [1 2 3; 4 5 6; 7 8 9] | ||
| + | A = | ||
| + | 1 2 3 | ||
| + | 4 5 6 | ||
| + | 7 8 9 | ||
| + | >> det(A) | ||
| + | ans = | ||
| + | 0 % -> лошо обоснована матрица | ||
| + | |||
| + | >> x = A\b | ||
| + | Warning: Matrix is close to singular or badly scaled. | ||
| + | Results may be inaccurate. RCOND = 1.541976e-18. | ||
| + | x = | ||
| + | -3.333333333333333 | ||
| + | 5.666666666666667 | ||
| + | -2.000000000000000 | ||
| + | |||
| + | == Eigen values lambda = eig(A) == | ||
| + | |||
| + | трептения на системи с няколко степени на свобода | ||
| + | |||
| + | A*x = lam*x | ||
| + | (A-lam*I)*x = 0 % homogenna | ||
| + | det(A - lam*I) = 0 % togava ima resheniq A[n][m] | ||
| + | a[1]lam^n + a[2]lam^(n-1) ... = 0 % edin polinom ot n stepen ima n re[eniq | ||
| + | lam[1], lam[2] ... - собствени стойности на матрицата А | ||
| + | |||
| + | за всяка собствена стойност има собствен вектор от решения | ||
| + | |||
| + | lambda = eig(A) | ||
| + | [X, L] = eig(A) | ||
| + | lambda[1] = L(1,1); lambda[2] = L(2,2) | ||
| + | |||
| + | '''Обощена задача на собствените стойности ''' | ||
| + | |||
| + | A*x = lam*B*x % Anxn, Bnxn | ||
| + | (A-lam*B)x = 0 | ||
| + | det(A-lam*B) = 0 | ||
| + | |||
| + | 0 | ||
| + | <code><pre> | ||
| + | >> A = [ 22 2 44; 2 3 10; 2 4 6]; | ||
| + | >> B = [33 2 7; 32 9 1; 2 8 10]; | ||
| + | >> [X L] = eig(A,B) | ||
| + | |||
| + | >> [X L] = eig(A,B) | ||
| + | |||
| + | X = | ||
| + | |||
| + | 0.3172 1.0000 -0.1075 | ||
| + | -1.0000 0.3641 1.0000 | ||
| + | 0.7838 -0.5667 -0.0095 | ||
| + | |||
| + | |||
| + | L = | ||
| + | |||
| + | 2.8282 0 0 | ||
| + | 0 -0.0742 0 | ||
| + | 0 0 0.4848 | ||
| + | |||
| + | </pre></code> | ||
| + | |||
| + | Проверка | ||
| + | >> (A - L(1,1)*B)*X(:,1) | ||
| + | ans = | ||
| + | 1.0e-13 * | ||
| + | -0.1421 | ||
| + | -0.1510 | ||
| + | -0.0355 | ||
| + | |||
| + | == Корени на алгебрични уравнения fzero() == | ||
| + | |||
| + | f(x) = 0; | ||
| + | |||
| + | x = fzero(@sin, 3) % 3 e началното приближение | ||
| + | x = | ||
| + | 3.1416 | ||
| + | |||
| + | x - tg(x) = 0 % da se namerqt pyrvite tri polozhitelni korena | ||
| + | |||
| + | x = -5 : 0.01 : 20; plot(x, (x-tan(x))); | ||
| + | x = -5 : 0.01 : 20; plot(x, (x.*cos(x)-sin(x))); | ||
| + | >> x1 = fzero('x.*cos(x)-sin(x)', [4 5]) | ||
| + | x1 = | ||
| + | 4.4934 | ||
| + | |||
| + | f(x) - kato string | ||
| + | |||
| + | f = inline('x.*cos(x)-sin(x)') | ||
| + | f = | ||
| + | Inline function: | ||
| + | f(x) = x.*cos(x)-sin(x) | ||
| + | |||
| + | == Минимум на една функция == | ||
| + | |||
| + | fminbnd('x.*cos(x)-sin(x)', -10, 10) | ||
| + | ans = | ||
| + | 3.1416 | ||
| + | |||
| + | == Числено пресмятане на определени интеграли quad() == | ||
| + | |||
| + | quad(@function(x), a, b); | ||
| + | |||
| + | quad(@function(x), a, b, eps); % tochnost | ||
| + | |||
| + | quad('1./(x.^3+5)', -0, 2, 1.e-15) | ||
[[Category:Matlab]] | [[Category:Matlab]] | ||
Latest revision as of 14:01, 19 April 2011
Contents
Стринг с апостроф
Когато искаме апостроф слагаме два апострофа!
ilian'co => ilian''co
>> ''diff''
??? ''diff''
|
Error: Unexpected MATLAB expression.
>> '''diff'''
ans =
'diff'
Масив от клетки
Всеки елемент може да е от различен тип
Cells = { 10, pi, 3+4i, 'MuPad', [1 2 3], [1 2 3; 4 5 6] , {'a', 1} }
Cells =
Columns 1 through 5
[10] [3.1416] [3.0000 + 4.0000i] 'MuPad' [1x3 double]
Columns 6 through 7
[2x3 double] {1x2 cell}
Достъп до всички данни на масива от клетки
for i = 1:6, Cells(i), end
Cells{6}{2}
Преобразувания на Лаплас
>> syms h w p k
>> syms t, ilaplace(h*w/((p^2+w^2)*(p^2+k^2)), p, t)
ans =
(h*sin(t*w))/((k + w)*(k - w)) - (h*w*sin(k*t))/(k*(k + w)*(k - w))
>> y = simplify(ans)
y =
(h*(k*sin(t*w) - w*sin(k*t)))/(k*(k^2 - w^2))
>> pretty(y)
h (k sin(t w) - w sin(k t))
---------------------------
2 2
k (k - w )
>>
syms p x, fi = ilaplace(1/(p-1)^2, p, x) fi = x*exp(x)
>> syms x p k w
>> f = exp(-k*x)*sin(w*x + k);
>> F = laplace(f, x, p)
F =
(sin(k)*(k + p) + w*cos(k))/((k + p)^2 + w^2)
>> syms t, pretty(simplify(F, p,x))
??? Error using ==> sym.simplify
Too many input arguments.
>> syms t, simplify(ilaplace(F, p,x))
ans =
sin(k + w*x)/exp(k*x)
Пример: ... няма го
>> syms x p ,laplace(exp(-x)*sin(2*x),x,p) ans = 2/((p + 1)^2 + 4)
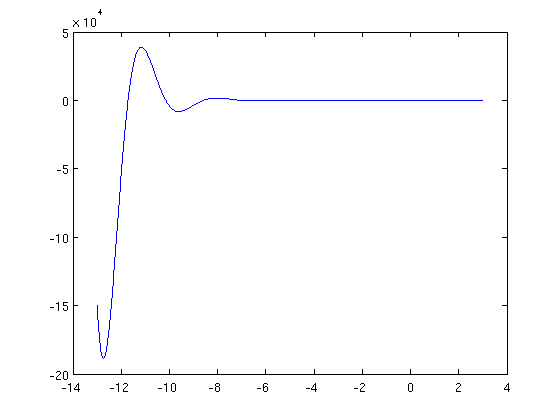
y = ilaplace(2*p/((p^2+p+1)*((p+1)^2+4)), p, x) plot(-13:0.01:3,subs(y,x, -13:0.01:3))
Проверка
>> diff(y,x) +y + int(subs(y,x,t),t,0,x) ans = (2*cos(2*x))/(13*exp(x)) - (8*(cos(2*x)/4 - 2*sin(2*x)))/(13*exp(x)) - (8*(cos((3^(1/2)*x)/2)/4 +
(3^(1/2)*sin((3^(1/2)*x)/2))/2))/(13*exp(x/2)) - (2*cos((3^(1/2)*x)/2))/(13*exp(x/2)) - (3*sin(2*x))/(13*exp(x)) + (4*(cos((3^(1/2)*x)/2) - (3^(1/2)*sin((3^(1/2)*x)/2))/6))/(13*exp(x/2)) + (14*3^(1/2)*sin((3^(1/2)*x)/2))/(39*exp(x/2))
>> simplify(ans) ans = sin(2*x)/exp(x)
Решаване системи линейни уравнения
A*x= B x = A\B % \ може да се прилага при правоъгълни матрици, при повече редове от колони се решава за средно квадратичната стойност
A = [3 7 5; 2 6 9; 4 4 4] A =
3 7 5
2 6 9
4 4 4
>> b = [2 3 4]'
b =
2
3
4
>> A\b
ans =
1.0500
-0.4500
0.4000
При лошо обоснована матрица може да има грешки
>> A = [1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> det(A)
ans =
0 % -> лошо обоснована матрица
>> x = A\b
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.541976e-18.
x =
-3.333333333333333
5.666666666666667
-2.000000000000000
Eigen values lambda = eig(A)
трептения на системи с няколко степени на свобода
A*x = lam*x (A-lam*I)*x = 0 % homogenna det(A - lam*I) = 0 % togava ima resheniq A[n][m] a[1]lam^n + a[2]lam^(n-1) ... = 0 % edin polinom ot n stepen ima n re[eniq lam[1], lam[2] ... - собствени стойности на матрицата А
за всяка собствена стойност има собствен вектор от решения
lambda = eig(A) [X, L] = eig(A) lambda[1] = L(1,1); lambda[2] = L(2,2)
Обощена задача на собствените стойности
A*x = lam*B*x % Anxn, Bnxn (A-lam*B)x = 0 det(A-lam*B) = 0
0
>> A = [ 22 2 44; 2 3 10; 2 4 6];
>> B = [33 2 7; 32 9 1; 2 8 10];
>> [X L] = eig(A,B)
>> [X L] = eig(A,B)
X =
0.3172 1.0000 -0.1075
-1.0000 0.3641 1.0000
0.7838 -0.5667 -0.0095
L =
2.8282 0 0
0 -0.0742 0
0 0 0.4848
Проверка
>> (A - L(1,1)*B)*X(:,1) ans = 1.0e-13 * -0.1421 -0.1510 -0.0355
Корени на алгебрични уравнения fzero()
f(x) = 0;
x = fzero(@sin, 3) % 3 e началното приближение x = 3.1416
x - tg(x) = 0 % da se namerqt pyrvite tri polozhitelni korena
x = -5 : 0.01 : 20; plot(x, (x-tan(x)));
x = -5 : 0.01 : 20; plot(x, (x.*cos(x)-sin(x)));
>> x1 = fzero('x.*cos(x)-sin(x)', [4 5])
x1 =
4.4934
f(x) - kato string
f = inline('x.*cos(x)-sin(x)')
f =
Inline function:
f(x) = x.*cos(x)-sin(x)
Минимум на една функция
fminbnd('x.*cos(x)-sin(x)', -10, 10)
ans =
3.1416
Числено пресмятане на определени интеграли quad()
quad(@function(x), a, b);
quad(@function(x), a, b, eps); % tochnost
quad('1./(x.^3+5)', -0, 2, 1.e-15)