Difference between revisions of "Числено интегриране"
| Line 93: | Line 93: | ||
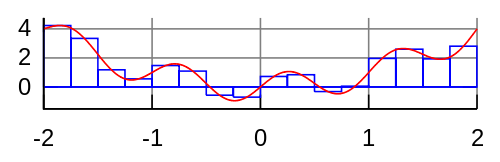
Правилото на трапеца няма как да е точно за големи интервали, но ако разглежданият интервал се раздели на по-малки интервали и се сумират техните стойности ще се получи сравнително точно заместване. Ако функцията f има втора производна то грешката от интегриране намалява с <math> h^2 </math>, където h e големината на интеграла. | Правилото на трапеца няма как да е точно за големи интервали, но ако разглежданият интервал се раздели на по-малки интервали и се сумират техните стойности ще се получи сравнително точно заместване. Ако функцията f има втора производна то грешката от интегриране намалява с <math> h^2 </math>, където h e големината на интеграла. | ||
| − | <math> \int_a^b f(x)dx | + | <math> \int_a^b f(x)dx \approx h \left ( frac{f(x_0)}{2} +f(x_1) + \dots + f(x_{n-1}) + frac{f(x_n)}{2} \right ) |
| − | + | ||
| − | f ( | ||
| − | + f ( | ||
| − | |||
| − | + | ||
| − | f ( | ||
| − | |||
| − | |||
</math> | </math> | ||
Revision as of 11:11, 6 January 2013
Contents
В числения анализ, числено интегриране определя група от алгоритми за намиране стойността на определен интеграл. Понятието се използва и при численото решаване на диференциални уравнения.
Идеята на численото интегриране е функцията f(x) да се приближи с подходяща функция φ(x), която по-лесно може да се интегрира. , където:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(x)} може да се интегрира точно
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r(x)} e остатъка (грешката - residual)
Най-често φ(x) е интерполационен полином построен по някакви възли в интервала Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b]} за Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} .
Числените методи за интегриране се налага да се използват:
- Когато не съществува примитивна функция за f(x) (интегралът не се изразява с елементарни функции)
- когато примитивната функция за f(x) е много сложен израз
Ако f(x) е плавно изменяща се функция, която може да се интегрира в малък брой измерения и има определени гранични стойности, съществуват редица методи с различна степен на точност за апроксимиране на интеграла Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)\,dx} .
Представяме интеграла по следния начин:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)\,dx = \sum_{i=1}^{n} A_i f(x_i) + R(f) }
.
Формули на Нютон-Коутс за числено интегриране
Пример. Да се пресметне по формулата на десните правоъгълници Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_2^3 \frac{ln(x)}{x}\,dx , n = 10 }
Решение. По условие Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,b] = [2,3]; n=10}
Метод на правоъгълниците
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = \frac{b - a}{n} = \frac{3-2}{10} = 0.1}
Съгласно Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I \approx \int_{a}^{b} = \int_{x_0}^{x_1} + \int_{x_1}^{x_2} + ... + \int_{x_{n-1}}^{x_n} = y_0 h + y_1 h +...+ y_{n-1} h = h \sum_{i=0}^{n-1} y_i}
x = {2, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3}
y = {0.346574, 0.353303, 0.35839, 0.362134, 0.364779, 0.366516,0.367504, 0.367871, 0.367721, 0.367142, 0.366204}.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I \approx h \sum_{i=0}^{n-1} y_i = 0.362193}
Аналитично решение
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_2^3 \frac{log(x)}{x} dx = 1/2 (log^2(3)-log^2(2)) \approx 0.363248}
Решение с Матлаб
h = 0.1 % step
m = 0; % sum
for i = 2:h:3-h
m = log(i)/i + m
end
I = m*h
I = 0.36219
Оценка на грешката
Грешка от интегриране: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert r_0 \vert \leq \left | \int_{x_0}^{x_1} R_0\,dx\ \right | \leq M_1 \left | \int_{x_0}^{x_1} (x-x_0)\,dx\ \right | = M_1 \frac{ (x-x_0)^2 }{2} \Bigg|_{x_0}^{x_1} = M_1 \frac{h^2}{2} = O(h^2) }
Сумарна грешка:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R \leq n*M_1 \frac{h^2}{2} = M_1 \frac{h(b-a)}{2} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1=\max\limits_{[2,3]}\vert f'(\xi)\vert}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=\frac{ln(x)}{x}} за Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{1-ln(x)}{x^2}}
Максималната стойност в [2,3] на Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{1-ln(x)}{x^2}} е при x = 2
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_1 = \frac{1 - ln(2)}{2^2} = 0.077 }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = M_1 \frac{h(b-a)}{2} = 0.077*0.1/2 = 0.004}
Анализ
Разликата от аналитичното решение и численото решение е Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.3632 - 0.3621 = 0.0011} , което е в рамките на максималната грешка.
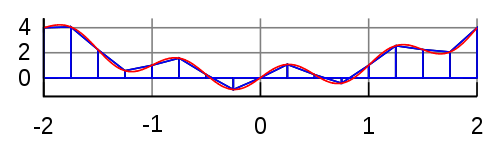
Формула на трапеца
Геометрично извеждане
Идеята на геометричното извеждане е да замести площта под кривата y = f(x) за x = a до х = b с площта на трапец ограничена от точките (a, 0), (b, 0), [a, f (a)], и [b, f (b)].
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x) \,dx \approx \frac{b-a}{2} \left [ f(a) + f(b) \right ]}
Правилото на трапеца няма как да е точно за големи интервали, но ако разглежданият интервал се раздели на по-малки интервали и се сумират техните стойности ще се получи сравнително точно заместване. Ако функцията f има втора производна то грешката от интегриране намалява с Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h^2 } , където h e големината на интеграла.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)dx \approx h \left ( frac{f(x_0)}{2} +f(x_1) + \dots + f(x_{n-1}) + frac{f(x_n)}{2} \right ) }