Difference between revisions of "Махало"
| Line 41: | Line 41: | ||
<math>\ell{d^2\theta\over dt^2} + g\sin\theta = 0 <=> \ell{d^2\theta\over dt^2} + g\theta = 0, \theta < 20^{\circ}</math> | <math>\ell{d^2\theta\over dt^2} + g\sin\theta = 0 <=> \ell{d^2\theta\over dt^2} + g\theta = 0, \theta < 20^{\circ}</math> | ||
| − | Полагаме <math> {\theta} = {y} </math> | + | Полагаме <math>\ {\theta} = {y} </math> |
<math> \ell{y''} + {g}{y} = 0 </math> | <math> \ell{y''} + {g}{y} = 0 </math> | ||
Revision as of 10:01, 29 June 2011
Цел: Създаване на връзки между диференциране и диференциални уравнения.
Постановка: Математическо махало. (Съпротивлението на въздуха се пренебрегва). Да се намери зависимостта на махалото спрямо времето, т.е. функцията на движение на махалато.
Анализ: Във всеки момент махалото се движи с различна скорост и ускорение, зависещи от ъгъла на отклонение на махалото.
Contents
Производни, разстояние, скорост и ускорение.
Движението на махалото се извършва по окръжност с радиус равен на дължината на нишката, на която е окачено махалото. От тук, следва че:
За да изразим скоростта ползваме първата производна (изменението на разстоянието за единица време). Изменя се само ъгълът, а дължината на нишката е константа и се запазва:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = {ds\over dt} = {{d\ell\theta}\over dt}= \ell {d\theta\over dt}}
По да изразим ускорението, използваме втората производна
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = {d^2s\over dt^2} = \ell{d^2\theta\over dt^2} } (1)
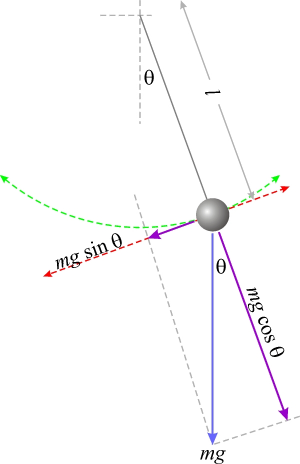
Сили действащи на махалото
Под внимание се взема само силата действаща по посока на движението. Допирателната по окръжността на движение (тангенциалната сила ( танго -> допир)). Перпендикулярната сила (нормалната ) се неутрализира.
От II закон на нютон Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = ma\,}
За махалото Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = gm \sin\theta = -ma\, => a = -g\sin\theta\, } (2)
Диференциално уравнение на махало
От (1) и (2) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle => -g\sin\theta = \ell{d^2\theta\over dt^2} <=> \ell{d^2\theta\over dt^2} + g\sin\theta = 0 }
Решаване на диференциалното уравнение
Има два подхода при решаване на диференциални уравнения, аналитичен и числен. При конкретното уравнение са възможни и двата подхода, но аналитичният метод може да се използва за Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta < 20^{\circ}} . В този случай диференциалното уравнение ще се преобразува в линейно от втори ред.
Аналаитично решение
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell{d^2\theta\over dt^2} + g\sin\theta = 0 <=> \ell{d^2\theta\over dt^2} + g\theta = 0, \theta < 20^{\circ}}
Полагаме Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ {\theta} = {y} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell{y''} + {g}{y} = 0 }